Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.2 - Ex. 1d

1. Esboce o gráfico da função F dada por

d) int_1^x f (t) d t onde f (t) = {[[0 s e t <= 1],[1 s e t > 1]])

Passo 1

Para esboçarmos o gráfico, precisamos integrar e ver qual o jeitão da função F ( x ) . Como f ( t ) é limitada e descontínua apenas no ponto t = 0 . Para integrar, vamos fazer o seguinte:

Se x <= 1 :

F (x) = int_1^x 0 d t

Se x > 1 :

F (x) = int_1^x 1 d t

Passo 2

Primeiro vamos ver para x <= 1 :

F (x) = int_1^x 0 d t

Integrando:

F (x) = 0 xx t |_0^1

Logo,

F (x) = 0

Agora vamos analisa o caso em que x > 1 :

F (x) = int_1^x d t

Resolvendo a integral:

F (x) = t |_1^x

Portanto,

F (x) = x - 1

Passo 3

Juntando tudo, temos:

F ( x ) = {[[0 , x <= 1],[x - 1 , x > 1]])

Fazendo um gráfico:

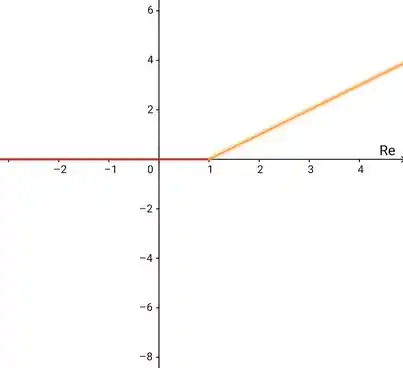
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calculeb)int_(- 1)^3 f (x) d x ondef (x) = {[[1 s e - 1 = x0],[x^2 s e 0x2],[0 s e 2 = x = 3]])
Calculeint_0^2 f (x) d x ondef (x) = {[[2 s e 0 = x1],[(1)/(x) s e 1 = x = 2]])
Calculea) ∫ 0 x f t d t o n d e f t = 1s e0 ≤ t10s et ≥ 1
Calculec) ∫ 0 x f t d t onde f t = t 2s e- 1 ≤ t ≤ 12s et1
Calculed) int_(- 2)^2 g (u) d u ondeg (u) = {[[(1)/(u^2) s e |u| = 1],[u s e |u|1]])