Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 10
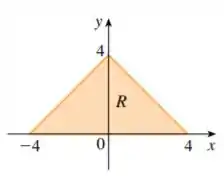
Escreva como uma integral iterada, onde é a região mostrada e é uma função arbitrária contínua em .
Passo 1
E aí meus queridxs, tudo bom com vocês? Pois bem, vamos entender o que tá acontecendo aqui nessa questão e o que ela deseja da gente. Ela pede pra gente descrever a integral como uma integral iterada onde é a região dada e uma função qualquer.
Vamos recordar os tipos de regiões que existem? Ora, a região do tipo I é quando a integral “varre” a figura verticalmente de uma função até a outra. Enquanto a de tipo II é horizontal.
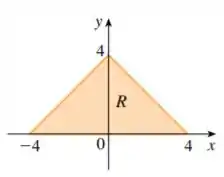
Veja que nesse caso nós teremos duas retas, e podemos “varrer” todo o gráfico indo da reta até a reta .
Nossa região é do tipo que poderemos descrever como a região entre as linhas e o eixo . Sendo assim, utilizando as coordenadas cartesianas podemos descrever a região como sendo
Passo 2
Com isso, nossa integral iterada será dada por
Pronto meus camaradas, só partir por abraço que a questão já foi resolvida. Sem muitos problemas, né?
