Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 37
Esboce o sólido cujo volume é dado pela integral iterada.
Passo 1
Faala, pessoal!
Essa questão da uma integral:
E pede pra esboçar o sólido que esse integral representa seu volume.
Vamos lembrar que o volume da região abaixo do gráfico da função em um domínio é dado por:
Então o que a gente vai fazer é descobrir quem é esse e esse , e desenhar!
Passo 2
Vamos identificar primeiro o domínio no plano . Observe que varia entre e enquanto varia entre e . Assim, o domínio de integração é representado por
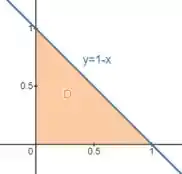
Essa é a região !
Passo 3
A função que está na integral é:
Ela representa a superfície:
Com isso, o sólido será a região abaixo dessa superfície sobre a região (no plano ).
Agora temos que olhar para o a superfície que é um plano.
Quando (eixo ), temos . Além disso quando , temos , ou seja, esse plano corta o plano exatamente na reta .
Vamos desenhar esse plano, no domínio :
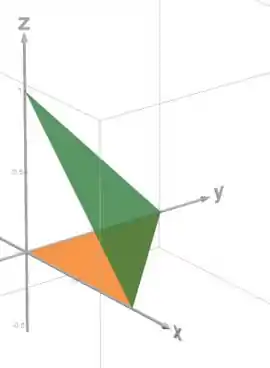
Em verde, temos o plano , e em laranja o domínio , no plano .
O nosso sólido vai ser a região entre as superfícies verde e laranja:
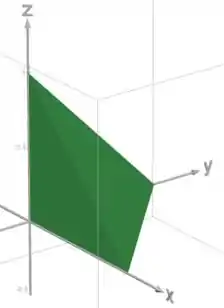
E esse é o nosso sólido!
Resposta
