Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 9

Escreva a equação em coordenadas esféricas.

x 2 + y 2 + z 2 = 9

Passo 1

Faaala pessoal, tudo na paz? Vamos lá!

Precisamos escrever a seguinte equação em coordenadas polares:

x 2 + y 2 + z 2 = 9

Vamos lembrar como é a equação e os respectivos valores de x , y e z em coordenadas polares:

x 2 + y 2 + z 2 = ρ 2

Onde,

x = ρ s e n   ϕ cos ⁡ θ

y = ρ s e n   ϕ   s e n   θ

  z = ρ cos ⁡ ϕ

Essas informações são extraídas ao se analisar um ponto P na esfera:

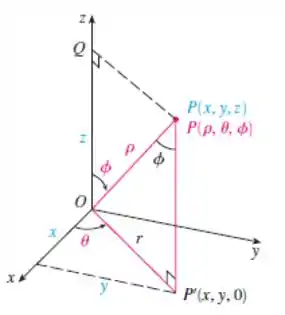
Sabendo disso, é só substituirmos na equação dada.

Vamos lá fazer isso! Partiu!!!

Passo 2

Das equações de transformação para coordenadas esféricas, temos:

  x 2 + y 2 + z 2 = ρ 2

x = ρ s e n   ϕ cos ⁡ θ

y = ρ s e n   ϕ   s e n   θ

  z = ρ cos ⁡ ϕ

A equação que devemos aplicar é:

x 2 + y 2 + z 2 = 9

Aplicando as equações de transformação, temos:

ρ 2 = 9 → ρ = 3

Pegamos somente o valor positivo de ρ , pois ele representa a distância e seria incoerente ter um valor menor que zero.

Agora iremos analisar a equação:

x 2 - y 2 - z 2 = 1

Substituindo os termos em coordenadas esféricas, temos:

ρ s e n   ϕ cos ⁡ θ 2 - ρ s e n   ϕ   s e n   θ 2 - ρ cos ⁡ ϕ 2 = 1

ρ 2 s e n 2 ϕ cos 2 ⁡ θ - s e n 2 θ - ρ 2 cos 2 ⁡ ϕ = 1

Agora precisamos lembrar de uma das propriedades trigonométricas, que:

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2

s e n 2   θ = 1 - cos ⁡ 2 θ 2

Substituindo, vamos ter que:

cos 2 ⁡ θ - s e n 2 θ = cos ⁡ 2 θ

Sendo assim, reescrevendo a equação anterior temos:

ρ 2 s e n 2 ϕ cos ⁡ 2 θ - ρ 2 cos 2 ⁡ ϕ = 1

E, colocando ρ 2 em evidência:

ρ 2 s e n 2 ϕ cos ⁡ 2 θ - cos 2 ⁡ ϕ = 1

Resposta

ρ = 3

ρ 2 s e n 2 ϕ cos ⁡ 2 θ - cos 2 ⁡ ϕ = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Identifique a superfície cuja equação é dada. ρ 2 sen 2 ⁡ ϕ sen 2 ⁡ θ + cos 2 ⁡ ϕ = 9
Descreva com palavras a superfície cuja equação é dada. ρ = 3
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ
Esfera e cilindro Encontre o volume do material cortado daesfera sólida r2 + z2 ≤ 9 pelo cilindro r = 3 sen u.
Coordenadas esféricas Encontre o volume da região delimitada pela superfície em coordenadas esféricas r = 2 sen f(veja a figura a seguir)