Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 11
Esboce o sólido descrito pelas inequações:
Passo 1
Iremos analisar as seguintes inequações:
Passo 2
Através da condição em , temos que ela representaria a esfera unitária caso não houvesse restrições para e , mas esse não é o caso! Então temos que a distância de qualquer ponto até essa superfície vale 1.
A restrição imposta para nos mostra que a superfície faz um ângulo de 30° com o eixo .
E, por último, a restrição em indica que a superfície não rotaciona totalmente ao redor de , mas sim, somente metade de uma volta completa.
Passo 3
Sendo assim, a superfície descrita é ilustrada a seguir:
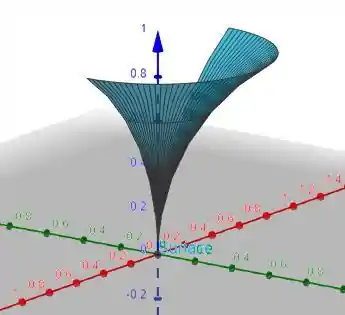
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Massa: encontre a massa do sólido delimitado pelas superfícies parabólicas z = 16 - 2 x 2 - 2 y 2 e z = 2 x 2 + 2 y 2 , se a densidade do sólido for δ x , y , z = x 2 + y 2 .
Uma região sólida no primeiro octante é delimitada pelos planos coordenados e pelo plano x + y + z = 2 . A densidade do sólido é δ x , y , z = 2 x
Um sólido no primeiro octante é delimitado pelos planos y = 0 e z = 0 e pelas superfícies z = 4 - x 2 e x = y 2 (veja a figura a seguir). Sua função de densidade é δ x , y , z = k x y , sendo k consta
As integrais anteriores sugerem que existem ordens preferenciais de integração para coordenadas esféricas, mas outras ordens fornecem o mesmo valor e são ocasionalmente mais fáceis de calcular. ∫ 0 2
As integrais anteriores sugerem que existem ordens preferenciais de integração para coordenadas esféricas, mas outras ordens fornecem o mesmo valor e são ocasionalmente mais fáceis de calcular. ∫ π 6