Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 13
Esboce o sólido descrito pelas inequações:
Passo 1
Iremos analisar as seguintes inequações:
Passo 2
Através da condição em , sabemos que a superfície deve ser uma região entre duas esferas, uma de raio 2 e outra de raio 4.
A restrição imposta para nos mostra que a superfície faz um ângulo, de no máximo, 60° a partir do eixo .
E, por último, a restrição em limita a superfície a parte positiva do plano .
Passo 3
Sendo assim, a superfície descrita é a região entre as duas superfícies esquematizadas a seguir:
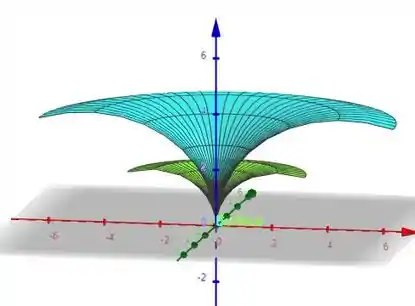
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Expresse o momento de inércia Iz do hemisfério sólido x2 +y2 + z2 ≤ 1, z ≥ 0, como uma integral iterada em coordenadas(a) cilíndricas e (b) esféricas. Em seguida, (c) encontre Iz
A porção superior cortada do sólido no Exercício 35 pelo plano xy.
O sólido delimitado pela cardioide de revolução r = 1 – cos f.
Cone e planos Encontre o volume do sólido delimitado pelocone z = 2x2 + y 2 entre os planos z = 1 e z = 2
Esfera e semiplanos Encontre o volume da região cortadada esfera sólida r ≤ a e pelos semiplanos u = 0 e u = p/6 noprimeiro octante.