Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.6 - Ex. 38

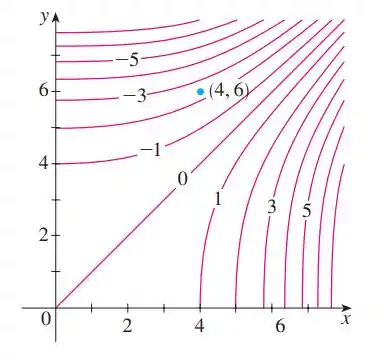
Esboce o vetor gradiente para a função para qual as curvas de nível são mostradas abaixo. Explique como você escolheu a direção e o sentido desse vetor.

Passo 1

Oie, abaixo a gente vai resolver essa atividade.

A gente tem aqui as curvas de nível da função e a gente precisa esboçar aqui o vetor gradiente:

Lembre-se que o vetor gradiente é dado por:

O vetor gradiente sempre aponta na direção do maior aumento da função, ou seja, perpendicular à superfície de nível.

Observando as superfícies de nível, percebemos que à medida que nos movemos perpendicularmente �� linha de nível, os valores aumentam. É a partir disso que iremos construir o que queremos.

Passo 2

Se colocarmos o ponto inicial do vetor gradiente em , o vetor será perpendicular a curva de nível de que inclui logo nós devemos esboçar uma porção da curva de nível através de e desenhar a linha perpendicular a curva neste ponto.

O vetor gradiente é paralelo a esta linha, que aponta na direção de funções crescentes. E com um comprimento igual ao máximo do valor da derivada direcional de em .

Podemos estimar este comprimento encontrando a taxa média de mudança de variação de direção do gradiente. A linha intersecta as linhas de contorno correspondentes a e e com distância estimada de unidades.