Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.6 - Ex. 8

Escreva uma equação polar de uma cônica com o foco na origem e com os dados fornecidos.

H i p é r b o l e ,           e x c e n t r i c i d a d e   3   ,           d i r e t r i z   r = - 6 cossec ⁡ θ

Passo 1

Olá, meu amigo. Vamos resolver mais uma atividade?!

Veja que temos aqui que escrever na forma polar a equação de uma elipse com excentricidade e = 3 e diretriz r = - 6 c o s s e c   θ .

As equações das cônicas polares dependem da diretriz, precisamos primeiro então avaliar a diretriz em coordenadas cartesianas para podermos avaliar qual equação utilizar, veja abaixo a figura para lhe ajudar melhor:

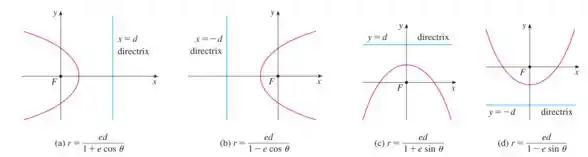
Depois de passarmos para coordenadas cartesianas e escolhermos nossa equação, fica mais tranquilo encontrar nossa equação polar.

r = - 6 cossec ⁡ θ

r = - 6   1 s e n   θ

r   s e n   θ = - 6

y = - 6

Passo 2

Vamos então dar continuidade a resolução, temos que:

r = - 6 cossec ⁡ θ

r = - 6   1 s e n   θ

E lembre-se da relação entre coordenadas cartesianas e polares:

y = r ⋅ sin ⁡ θ

Temos então:

r   s e n   θ = - 6

y = - 6

Show! Agora que a gente sabe como é a reta diretriz, podemos escrever a fórmula de cônicas com “ - e   s e n   θ ”:

r = e d 1 - e   s e n   θ

Bora substituir os valores?

e = 3

d = 6

r = 3 ⋅   6 1 - 3   s e n   θ

r = 18 1 - 3   s e n   θ

Beleza?

Resposta

r = 18 1 - 3   s e n   θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre uma equação polar para a curva representada pela equação cartesiana dada. x 2 + y 2 = 9
Encontre uma equação polar para a curva representada pela equação cartesiana dada. x = - y ² ²
Encontre uma equação polar para a curva representada pela equação cartesiana dada. y = 2 x - 1
Para cada uma das curvas descritas, decida se a curva seria mais facilmente dada por uma equação polar ou por uma equação cartesiana. Então, escreva uma equação para a curva.Uma reta que passa pela or
Para cada uma das curvas descritas, decida se a curva seria mais facilmente dada por uma equação polar ou por uma equação cartesiana. Então, escreva uma equação para a curva.Um círculo com raio 5 e ce