Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 39
Use um sistema de computação algébrico para determinar o volume exato do sólido.
Abaixo da superfície e acima da região limitada pelas curvas e para .
Passo 1
Faaala galerinha, tudo bem?
Precisamos determinar o volume exato de um sólido usando um sistema de computação algébrico.
Esse sólido está abaixo da superfície e acima da região limitada pelas curvas e para .
Primeiro vamos lembrar como é a expressão do volume:
Onde, é a função que delimita a região, e é nossa região de integração.
Precisamos montar nossa integral de volume, e já conhecemos z(x,y), pois o problema nos forneceu:
Precisamos encontrar nossa região , que compreende os intervalos de integração.
Vamos fazer o gráfico das curvas dadas para :
Assim conseguimos compreender o intervalo de variação de e .
Para resolver a integral, você pode usar a calculadora online WolframAlpha.
Bora colocar mão na massa!
Passo 2
Primeiro vamos construir os gráficos das curvas:
para .
Utilizando o software Geogebra, podemos obter o seguinte gráfico:
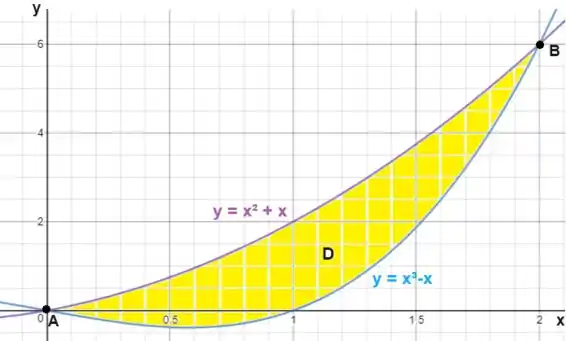
Nossa região de interesse é a região (em amarelo), que está entre as duas curvas.
Temos que o ponto e o ponto valem:
Observe que temos uma região do tipo I:
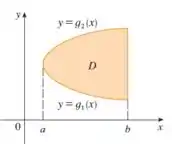
Logo, podemos escrever como:
Assim, o volume é dado por
Passo 3
Agora, precisamos determinar o volume através de um sistema de computação algébrico.
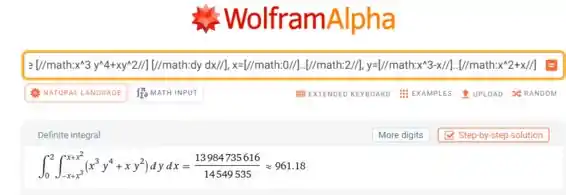
Fazendo a integral exata usando a calculadora do WolframAlpha, vamos obter:
Use o imput:
integrate [//math:x^3 y^4+xy^2//] [//math:dy dx//], x=[//math:0//]..[//math:2//], y=[//math:x^3-x//]..[//math:x^2+x//]
