Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 16.4 - Ex. 1 a
Estude a função dada com relação a máximo e mínimo no conjunto dado.
- no conjunto de todos tais que e
Passo 1
Perceba que a função não tem pontos críticos, então, vamos ter que analisar os pontos de fronteira, beleza?
Para nos ajuda, vamos fazer um desenho de região e identificar o pontos que precisamos, de acordo com o seguinte:
Como y-x
Como x+y
Para entendermos onde as retas se cruzam, teremos que 3x-y=0, 3x=y.
Logo, teremos o seguinte:
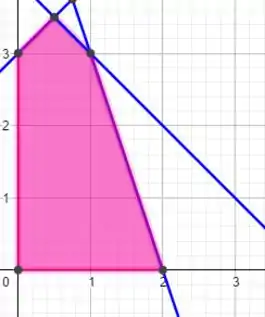
Passo 2
Perceba que nossos pontos de fronteira são . Vamos aplicar neles,
Ou seja, x
Sendo assim, . São máximo e mínimo respectivamente.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
3-Encontre o máximo e mínimo absoluto de cada uma das seguintes funções:b) f x ,y = x 3 + y 3 - 3 x y , na região triangular de vértices0 ,0 ,0 ,1e1 ,0 .
5. De uma longa folha de alumínio com 12 cm de largura, deseja-se construir uma calha , dobrando-se os lados da folha para cima e formando duas abas de mesmo tamanho , de modo que essas abas façam o m
4 . Em um laboratório foram obtidas, experimentalmente, as seguintes medidas t 1 = 0,v 1 = 2 t 2 = 1,v 2 = 8 t 3 = 2,v 3 = 11 Determine os coeficientes a e b da função v t = a t + b de modo a minimiza
Encontre o máximo e mínimo absoluto de cada uma das seguintes funções 3.c f x , y = e x 2 + y 2 + y x ≤ 1; y ≤ 1
6-Num círculo de raio R, traçam-se duas cordas paralelas, em cima e outra abaixo do centro, e constrói-se um trapézio isósceles. Determinar as distâncias das duas cordas ao centro, para que a área do