Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 4b
Passo 1
Lá vamos nos aventurar em mais uma integral!!
Cara, vamos fazer um esboço dessa região pra gente ver o que ta acontecendo.
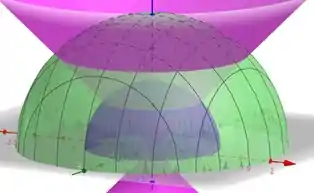
A nossa região W nessa questão é a parte de dentro do cone que engloba a esfera menor e a esfera maior. Observe que a gente ta pegando só a parte positiva do plano.
Passo 2
Beleza, agora a gente já conhece a região em que vamos integrar. Vamos usar nessa questão uma mudança de coordenadas esféricas, daí:
E seu jacobiano sendo dado por .
Em , teremos que sua variação será da esfera menor para a esfera maior, assim:
Ou seja, .
Nossa região está em torno de todo o eixo y, ou seja, rotacionou o plano todo, daí .
O cone é um cone que parte da origem, ele pode ser obtido através da rotação da reta , ou seja, corta o quadrante no meio, olha só:
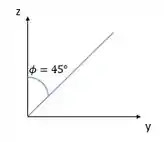
Assim, teremos que nossa variação em será de .
Passo 3
Agora que temos os intervalos de integração, podemos partir pra parte que resolvemos a integral, daí:
Aqui, vamos aplicar uma substituição simples, chamando , daí:
Resposta
Assim, a resposta da integral será .