Nos exercícios a , calcular a integral indefinida.
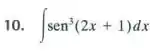
Passo 1
Aplicando o método da substituição simples com e , tem-se:
Para resolver essa integral, algumas identidades trigonométricas devem ser lembradas. Neste caso, será usada a relação que se usada na integral:
A primeira integral pode ser resolvida diretamente. Já a segunda requer o uso da substituição simples. Fazendo e :
Como a integral é indefinida, deve-se adicionar uma constante arbitrária ao resultado da integral.
Passo 2
Retornando a variável original: