Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 7.4 - Ex. 30

Nos exercícios 1 a 35 , calcular a integral indefinida.

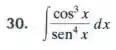
Passo 1

Para iniciar o exercício, pode-se reescrever a integral utilizando a identidade trigonométrica:

c o s 2 x = 1 - s e n 2 x

Tal que:

I = ∫ c o s x s e n 4 x 1 - s e n 2 x d x = ∫ c o s x s e n 4 x d x - ∫ c o s x s e n 2 x d x

Passo 2

Para resolver ambas as integrais, pode-se aplicar o método da substituição com u = s e n x e d u = c o s x d x :

I = ∫ 1 u 4 d u - ∫ 1 u 2 d u

I = - 1 3 u 3 + 1 u + C

Passo 3

Substituindo de volta para a variável original, tem-se:

I = - 1 3 s e n 3 x + 1 s e n x + C

Resposta

- 1 3 s e n 3 x + 1 s e n x + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral. ∫ t g 5 4 x sec 4 ⁡ ( 4 x )
Calcule a integral. ∫ s e n 2 2 x cos 3 ⁡ 2 xd x
Calcule a integral. ∫ sec 2 ⁡ θ ) t g 3 θ - t g 2 θ d θ
Calcule a integral. ∫ x cos ⁡ 3 x d x
Calcule a integral. ∫ 0 π / 4 tan 7 ⁡ θ d θ