Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.1 - Ex. 9
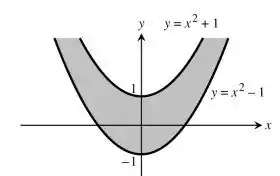
Nos Exercícios 5-12, encontre e esboce o domínio para cada função.
Passo 1
Fala galerinha tranquilidade, nesse exercício o que temos que fazer é avaliar o domínio da função, vamos considerar no conjunto dos números reais, então cada tipo de função tem um formato diferente, então como cada caso é um caso.
Passo 2
Nesse caso, temos uma função trigonométrica inversa, como é uma função arco cosseno, temos que compreender que ela só existe nos limites +1 e -1, então temos que avaliar dentro do argumento da seguinte forma:
Podemos isolar o para avaliar o esboço ficando:
Passo 3
Como a função arco cosseno tem um formato diferente dos que estamos acostumados em um contexto geral, com isso sugiro que use algum tipo de programa que gere gráificos, com isso vai ficar mais fácil de avaliar. Mas de qualquer forma, podemos imaginar o esboço
Temos duas parábolas nas extremidades, uma com coeficiente independente e outro com , ou seja temos duas parábolas com boca pra cima e uma corta mais em cima e outra mais embaixo o eixo dos , assim:
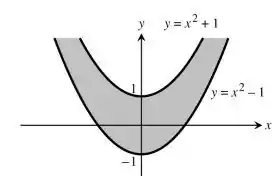
Resposta
