Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.1 - Ex. 10
Nos Exercícios 5-12, encontre e esboce o domínio para cada função.
Passo 1
Fala galerinha tranquilidade, nesse exercício o que temos que fazer é avaliar o domínio da função, vamos considerar no conjunto dos números reais, então cada tipo de função tem um formato diferente, então como cada caso é um caso.
Passo 2
Em um dos problemas anteriores fizemos do problema do ln, nesse caso é igual não podemos ter valor negativos e nem zero dentro do argumento significando que:
Para ficar mais fácil de visualizar podemos fazer uma fatoração ficando:
Passo 3
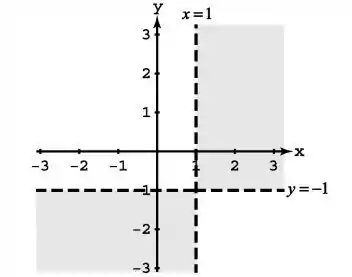
Nesse caso, nós temos que o dominio para que essas duas retas, uma em função de y e outra em função de x só tenha valores positvos resultado no gráfico.
Resposta
Duas retas com valores positivos e diferentes de zero:
Exercícios de Livros Relacionados
Calcule u → t ⋅ v → ( t ) , onde u → t = sen ti → + cos tj → + tk → e v → t = sen ti → + cos t j → + k → .
Sejam F → t = t , sen t , 2 e G → t = 3 , t , t 2 . Calcule e - tF → t
Sejam F → t = t , sen t , 2 e G → t = 3 , t , t 2 . Calcule F → t ×G → t
Sejam F → ,G → ,H → três funções definidas em A ⊂ R e a valores em R 3 . Verifique que F → ⋅ G → + H → = F → ⋅ G → + F → ⋅ H →
Sejam F → t = t , sen t , 2 e G → t = 3 , t , t 2 . Calcule F → t - 2G → t