Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.1 - Ex. 6
Nos Exercícios 5-12, encontre e esboce o domínio para cada função.
Passo 1
Fala galerinha tranquilidade, nesse exercício o que temos que fazer é avaliar o domínio da função, vamos considerar no conjunto dos números reais, então cada tipo de função tem um formato diferente, então como cada caso é um caso.
Passo 2
Nesse caso temos uma função baseada em um logaritmo natural, e para esse domínio só temos duas indeterminação é que o resultado dentro do logaritimo não pode ser zero, nem negativo, com isso nosso conjunto tem que ser maior que zero:
Resolvendo:
Passo 3
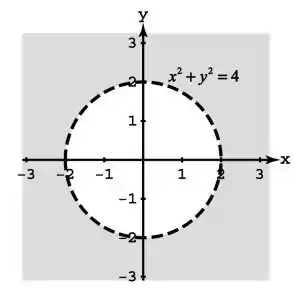
Com o resultado acima, podemos esboçar o gráfico para os valores maiores que zero, puxando um pouco de geométria análitica, essa função resultando é um circulo, porém só queremos a parte externa, porque não posso ter zero nem valores negativos
Resposta
O domínio da função são todos valores reais que estão fora do círculo de raio 2
