Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.1 - Ex. 3f
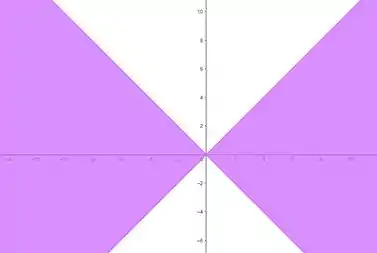
Represente graficamente e o domínio da função dada por
f)
Passo 1
Vamos analisar o domínio, ou seja, para quais valores não temos problema em aplicar a função.
Para que a função em f), para valores reais não tenha problema, precisamos que o que está dentro das raízes seja positivo, ou seja
Isso é,
Passo 2
Vamos analisar algumas possíveis situações:
- Se , então e . O que significa que teremos
Geometricamente, estamos com a região abaixo da reta para
- Se e então e . O que significa que teremos
Geometricamente, estamos com a região acima da reta para e
- Se e então e . O que significa que teremos
Geometricamente, estamos com a região acima da reta para e
- Se e então e . O que significa que teremos
Geometricamente, estamos com a região abaixo da reta para e
A interseção entre essas 4 regiões nos fornece o nosso domínio.
Resposta
