Represente graficamente o domínio da função dada por:
Passo 1
Definir o domínio da função:
A única restrição que temos é que :
Logo ,
Sendo assim ,
}
Passo 2
Representar o domínio graficamente, ou seja :
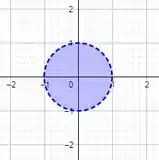
Resposta
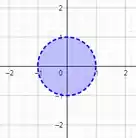
Represente graficamente o domínio da função dada por:
Definir o domínio da função:
A única restrição que temos é que :
Logo ,
Sendo assim ,
}
Representar o domínio graficamente, ou seja :

