Se , seja .
Se e são bolas inscrita e circunscrita a , respectivamente mostre que
Passo 1
Bom galera, vamos começar notando que temos as regiões:
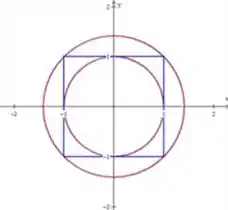
As áreas das regiões podem ser calculadas por integral, bem assim:
Mas a gente não precisa calcular, por que com o gráfico a gente já pode concluir que:
Passo 2
Belezinha, logo a gente também pode deduzir que:
Logo também podemos escrever:
E prontinho. 😊
Resposta
Ei, a resposta está no passo a passo :)