Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.6 - Ex. 68
- Mostre que a função é contínua e suas derivadas parciais e existem na origem, mas as derivadas direcionais em todas as outras direções não existem.
- Traçe o gráfico de perto da origem e comente como ele confirma a parte (a).
Passo 1
Oie, tudo bem? Vamos resolver juntos essa atividade.
Aqui a gente tem a seguinte função:
E a gente quer mostrar que ela é continua, também queremos mostrar que suas derivadas parciais existem na origem, isso é, em .
Para mostrar que ela é contínua iremos analisar o domínio da função. Já para as derivadas direcionas, iremos calcular o limite na origem utilizando a definição de limite e iremos também calcular para um local qualquer fora da origem também utilizando a definição, assim iremos analisar o comportamento das derivadas.
As derivadas parciais pela definição é dada por:
E :
Já a derivada direcional na direção de um vetor unitário é dada pelo limite:
Passo 2
(a) Podemos analisar a continuidade da função pelo seu domínio, neste caso, o domínio de é todo o , e não existe nenhum ponto onde a função não está definida, portanto podemos dizer que ela é contínua em todo o seu domínio.
Calculando as derivadas parciais na origem:
Substituindo a função:
Simplificando:
Temos então o resultado:
Agora em relação a :
Substituindo na função:
Temos então:
Passo 3
Agora se tivermos uma direção unitária qualquer, temos que a derivada direcional é
Colocando na função:
Separando em duas raízes:
Teremos então:
O limite varia entre mais ou menos infinito, dependendo de qual lado a gente se aproxima de , então a derivada direcional não existe.
Passo 4
(b) O gráfico de será feito utilizando o GeoGebra, para que possamos analisar o comportamento da função e responder o que nos foi pedido:
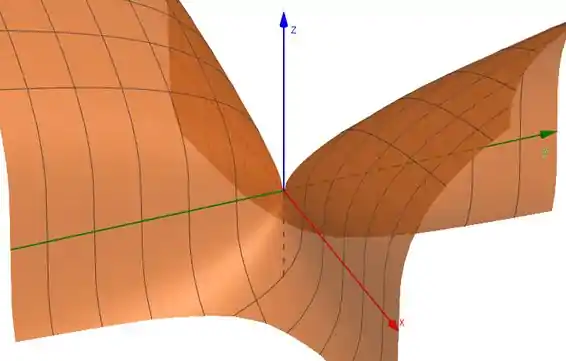
Podemos perceber o comportamento que calculamos nos limites, para as derivadas direcionais, próximo da origem temos que a função cresce, ou diminui a uma taxa muito elevada.
Resposta
Ver o desenvolvimento