Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.4 - Ex. 2d
Nos exercícios de a , denota o vetor posição de uma partícula se movendo, em cada instante . Em cada caso, determine:
2)
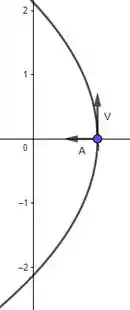
d) dois vetores tangentes unitários à trajetória da partícula em . Trace um esboço da trajetória da partícula e represente geometricamente os vetores e
Passo 1
Pô galera, todo vetor velocidade é tangente ao vetor posição em qualquer instante de tempo. Quer vetor tangente? Vamos então fazer:
Que nesse caso será:
Aplicando , temos:
E veja só, o vetor é um vetor com mesma direção do vetor mas sentidos opostos. Isso na prática quer dizer que ele também é um vetor tangente! Dois vetores tangentes então são:
Mas como queremos vetores unitários, temos que dividir ambos pelo módulo de cada um! Por sorte só vamos precisar calcular uma vez já que o módulo deles é igual:
Os vetores unitários serão então:
Passo 2
Pra fazer um esboço da trajetória a melhor forma é manipular a parametrização pra sair uma equação cartesiana. Veja que nela, temos:
O que é o mesmo que:
Igualando as duas equações:
Olhando bem pra essa equação, lembra uma equação de uma parábola, só que com o e o trocado de lado. Oras, só esboçar uma parábola deitada! Tá na mão:
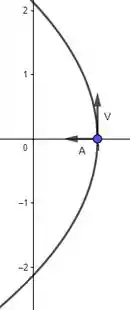
Resposta
