Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.5 - Ex. 2

Nos Exercícios 1-6, encontre o gradiente da função no ponto determinado. Em seguida, esboce o gradiente juntamente com a curva de nível que passa pelo ponto.

f x ,   y = ln ⁡ x 2 + y 2 ,     1 ,   1

Passo 1

Olá galerinha, vamos lá encarar este exercício juntos!

O vetor gradiente de f x ,   y em um ponto P 0 x 0 ,   y 0 é o vetor

∇ f = ∂ f ∂ x i + ∂ f ∂ y j

obtido por meio do cálculo das derivadas parciais de f em P 0 .

Do enunciado temos a seguinte função:

f x ,   y = ln ⁡ x 2 + y 2

Sabemos que:

y = ln ⁡ u → y ' = u ' u

A derivada da função f em relação a x é u = x 2 + y 2 u ' = 2 x                   , logo:

∂ f ∂ x = 2 x x 2 + y 2

E em relação a y u = x 2 + y 2 u ' = 2 y                   :

∂ f ∂ y = 2 y x 2 + y 2

Sendo assim, nosso gradiente é:

∇ f = 2 x x 2 + y 2 i + 2 y x 2 + y 2 j

Substituindo nosso ponto do enunciado 1 ,   1 :

∇ f = 2 ∙ 1 1 2 + 1 2 i + 2 ∙ 1 1 2 + 1 2 j

∇ f = 2 2 i + 2 2 j

∇ f = i + j

Passo 2

Além disso, no ponto 1 ,   1 , temos:

f x ,   y = ln ⁡ x 2 + y 2 = ln ⁡ 1 2 + 1 2

f x ,   y = ln ⁡ 2

Ou seja:

ln ⁡ x 2 + y 2 = ln ⁡ 2

x 2 + y 2 = 2

É uma circunferência com r = 2 . Logo:

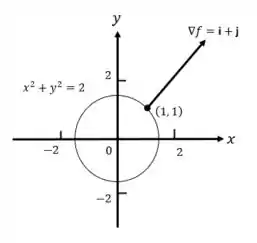
Até mais pessoal.

Resposta

  • ∇ f = i + j ;
  • x 2 + y 2 = 2 .

Exercícios de Livros Relacionados

Erro carregado na mudança de coordenadasa. Se x = 3 ± 0,01 e y = 4 ± 0,01, conforme mostrado, comaproximadamente qual precisão você pode calcular ascoordenadas polares r e u do ponto P(x, y) a partir
Gradiente ortogonal à tangente Suponha que uma função diferenciável f ( x , y ) tenha o valor constante c ao longo de uma curva diferenciável x = g ( t ) , y = h ( t ) ; ou seja, f ( g ( t ) , h ( t )
Extremos sobre uma superfície Mostre que os únicos má-ximos e mínimos possíveis de z sobre a superfície z = x3 +y3 – 9xy + 27 ocorrem em (0, 0) e (3, 3). Mostre que nem um máximo nem um mínimo ocorre
Caminho de uma partícula atraída pelo calor Uma partícula atraída pelo calor tem a propriedade de, em qualquer ponto (x, y) no plano, mover-se na direção de máximo aumento da temperatura. Se a tempera
Curva tangente a uma superfície Mostre que a curva r ( t ) = t 3 4 - 2 i + 4 t - 3 j + c o s ⁡ ( t - 2 ) k é tangente à superfíciex 3 + y 3 + z 3 - x y z = 0