Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.Exercícios práticos - Ex. 78
Nos Exercícios 73-78:
a. Utilize séries de potências para avaliar o limite.
b. Em seguida, utilize um gráfico para provar seus cálculos.
Passo 1
Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?
(a)
Usando a série de potência das funções e , temos:
(b)
Graficamente, destacado pela reta vermelha, temos a comprovação do limite encontrado:
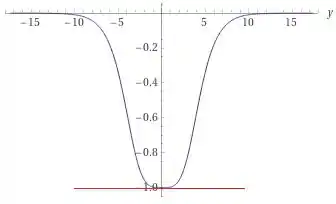
Espero ter ajudado! Abraços e até a próxima!
Resposta
. Veja o gráfico acima.
Exercícios de Livros Relacionados
Nos Exercícios 41-48, utilize o Teorema 20 para encontrar o intervalo de convergência da série e, dentro desse intervalo, a soma da série como uma função de x. ∑ n = 0 ∞ x - 1 2 n 4 n
Nos Exercícios 41-48, utilize o Teorema 20 para encontrar o intervalo de convergência da série e, dentro desse intervalo, a soma da série como uma função de x. ∑ n = 0 ∞ 3 n x n
Nos Exercícios 41-48, utilize o Teorema 20 para encontrar o intervalo de convergência da série e, dentro desse intervalo, a soma da série como uma função de x .46. ∑ n = 0 ∞ ln x n
A série sec x = 1 + x 2 2 + 5 24 x 4 + 61 720 x 6 + 277 8064 x 8 + … Converge para sec x para - π 2xπ 2 . a. Encontre os cinco primeiros termos de uma série de potências para a função ln sec x
Nos Exercícios 41-48, utilize o Teorema 20 para encontrar o intervalo de convergência da série e, dentro desse intervalo, a soma da série como uma função de x .48. ∑ n = 0 ∞ x 2 - 1 2 n