Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.4 - Ex. 1b
Determine a região de integração D e troque a ordem de integração das seguintes integrais
b.
Passo 1
Oii, estamos agora embarcando no mundo das integrais. Como você muito bem sabe, uma interpretação geométrica de integrais é o cálculo de áreas. Assim os intervalos de integração nos dizem que região do Plano estamos. E olha que bacana. Não importa a ordem de integração o valor final SEMPRE tem que ser o mesmo. Assim podemos ser bacana em algumas ocasiões nós manipularmos quais variáveis vamos integrar primeiro, pense sempre em poupar esforço!
Passo 2
No nosso caso temos
Vamos começar pela intepretação mais fácil. Y varia da curva ate a curva . Então sabemos que y esta entre a seguinte região
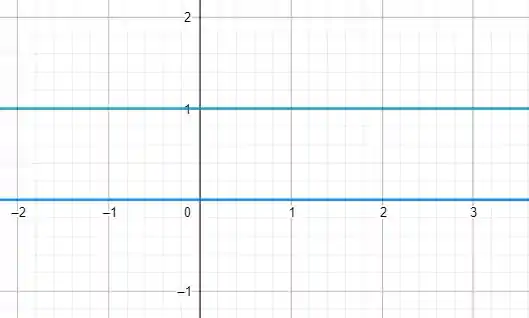
Agora temos que ver x, porque x varia da curva ate a curva . Então podemos concluir que a região é
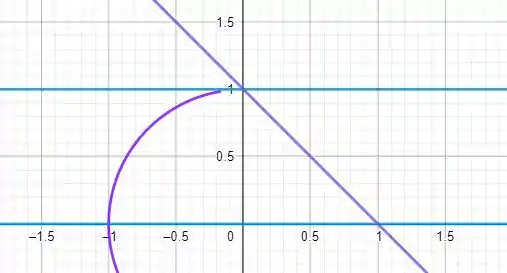
A região central, interseção das 4 curvas. Agora temos que inverter a região, podemos então fazer x variar entre . O problema é y, pois temos que y começa com a reta e ao longo da região toda y é limitado superiormente por 2 curvas diferentes. E chegamos a conclusão que Não temos como fazer.
A solução é repartir essa integral em 2. Com x variando entre e assim conseguimos colar apenas uma função limitando y superiormente. Sendo que agora as curvas têm que ser funções de x. Vamos inverter essas funções
Como queremos o segundo quadrante temos que optar pela raiz positiva. Agora o outro limite de y
Com isso nossa integral fica
Terminamos por aqui. Pode comemorar! \o/
Te vejo na próxima resolução
: )