Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.4 - Ex. 4a
Transforme a soma das integrais duplas
Em uma única integral dupla numa região conveniente.
Passo 1
E aí, galerinha!! Vamos lá com mais um exercício com o Responde Aí!! :D
Como no nosso caso ambas as integrais duplas representam uma região do tipo , em que a região é contínua em e possui limitada por funções de , podemos transformá-las em uma única região do mesmo tipo. Mas para ajudar nisso e termos certeza disso, vamos fazer o esboço da interseção dessas regiões e determinar os intervalos de integração para cada variável.
Passo 2
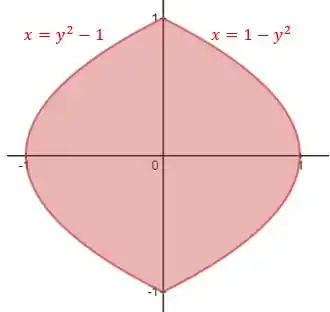
Então, se fizermos o desenho das regiões representadas pela primeira e segunda integral, respectivamente, temos:
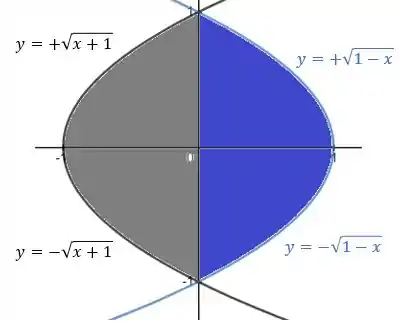
Para as curvas, temos que encontrar uma função geral que represente toda a região da primeira integral para ser o limite de integração inferior. Sabemos que a região é representada por:
Elevando ambos os lados da equação ao quadrado:
E isolando :
O mesmo para a região da segunda integral para que represente o limite de integração superior. Temos que ela é dada por:
Elevando ao quadrado:
Isolando novamente:
Com isso, o intervalo de pode ser dado por:
Visto que deixamos limitada por funções de , isso significa que a nossa região agora é do tipo e deve ser contínua em . Então, se olharmos o esboço, podemos escrever como:
Passo 3
Dessa forma, podemos juntar ambas as integrais e escrever:
Tal que se formos esboçar a região da nova integral, conseguimos ver que é a interseção das regiões representadas por cada integral:
