Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 38
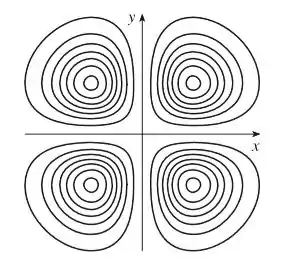
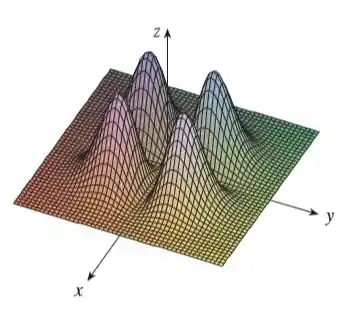
Faça um esboço de um mapa de contorno da função cujo gráfico está mostrado.
Passo 1
E aí, pessoal. Tudo certo? Vamos resolver mais uma questão.
A questão nos deu o gráfico de uma função de duas variáveis e quer o mapa de contorno da função.
O mapa de contorno de uma função é formado pelo conjunto das curvas de nível de uma função.
As curvas de nível são as curvas tais que
Ao traçar uma curva de nível, basicamente estamos cortando o gráfico de na horizontal.
Pegou a ideia? Então vem comigo!
Passo 2
Como já falamos no “Passo 1”, o mapa de contorno é feito como se fosse a projeção do gráfico da função no plano .
Nesse caso serão 4 conjuntos de curvas circulares, uma em cada quadrante do plano . Assim:
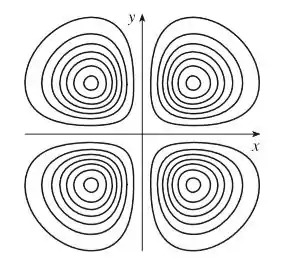
Resposta
Exercícios de Livros Relacionados
Encontre e esboce o domínio da função. f x , y = y - x 2 1 - x 2
Esboce o gráfico da função. f x , y = 10 - 4 x - 5 y
Encontre e esboce o domínio da função.f (x , y) = ln ( 9 - x^2 - 9 y^2 )
Encontre e esboce o domínio da função.f (x , y , z) = ln ( 16 - 4 x^2 - 4 y^2 - z^2 )
Esboce o gráfico da função.f (x , y) = y