Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.6 - Ex. 64

  1. O plano y + z = 3 intercepta o cilindro x 2 + y 2 = 5 em uma elipse. Encontre as equações paramétricas para a reta tangente a essa elipse no ponto 1,2 , 1 .
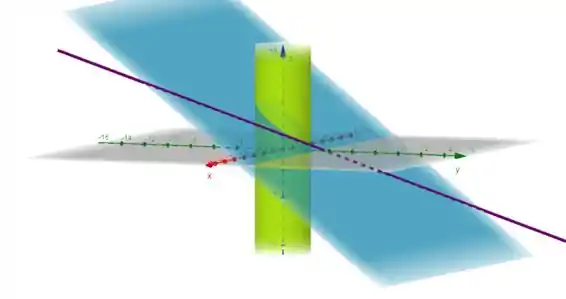
  2. Plote o gráfico do cilindro, do plano, e da reta tangente na mesma tela

Passo 1

Olá, meu querido amigo. Vamos resolver essa atividade juntos.

Temos

f x , y , z = y + z

e

g x , y , z = x 2 + y 2

Nesta tarefa, precisamos encontrar as linhas tangentes à elipse, que é a linha tangente ao plano e ao cilindro no ponto dado.

Primeiramente, calcularemos o gradiente do cilindro no ponto dado e o normal do plano, como são perpendiculares às retas tangentes calcularemos então o produto vetorial.

O gradiente do cilindro será dado por:

∇ G

E o gradiente do plano por:

∇ F

Passo 2

A linha tangente a elipse será perpendicular tanto a ∇ F quando ∇ G , então vamos calcular esses gradientes:

Dado que:

F x , y , z = y + z

As suas derivadas parciais são:

F x = 0

F y = 1

F z = 1

Sendo assim:

∇ F 1,2 , 1 = 0,1 , 1

Já que o vetor gradiente é constante para todos os pontos.

Agora para G iremos repetir o procedimento, iremos derivar parcialmente para todas as variáveis e iremos encontra o gradiente no ponto requerido:

G x , y , z = x 2 + y 2

F x = 2 x

F x 1,2 , 1 = 2

E:

F y = 2 y

F y 1,2 , 1 = 4

Por ultimo vamos para:

F z = 0

Agora a gente precisa realizar o produto vetorial, como falamos, a reta tangente será paralela ao vetor ∇ F 1,2 , 1 × ∇ G 1,2 , 1 :

∇ F 1,2 , 1 × ∇ G 1,2 , 1 = i j k 0 1 1 2 4 0

Calculando o determinante:

∇ F 1,2 , 1 × ∇ G 1,2 , 1 = i 1 1 4 0 - j 0 1 2 0 + k 0 1 2 4

∇ F 1,2 , 1 × ∇ G 1,2 , 1 = - 4,2 , - 2

A equação da reta é então dada por:

γ t = P + t ∇ F 1,2 , 1 × ∇ G 1,2 , 1

Vamos substituir:

γ t = 1,2 , 1 + t 4 , - 2,2

Parametrizando:

x t = 4 t + 1

y t = - 2 t + 2

z t = 2 t + 1

Passo 3

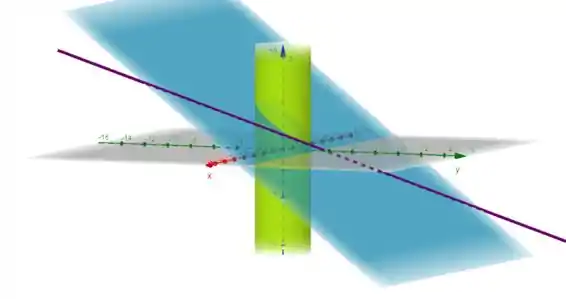
Com ajuda do GeoGebra, conseguimos plotar todo mundo no mesmo plano tridimensional:

b

Resposta

x = 1 + 4 t ; y = 2 - 2 t ; z = 1 + 2 t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja S a superfície de equação z = 2 - x 2 - x y + y 2 4 . b ) Escreva as equações da reta normal à S que é paralela à reta L .
Determine uma equação do plano tangente e uma equação da reta normal ao hiperbolóide de equação x 2 - 2 y 2 - 4 z 2 = 10 no ponto 4 ,- 1 ,1 .
Considere a curva C de intersseção das superfícies definidas de equações x 2 - 2 x z + y 2 z = 3 e 3 x y - 2 y z = - 2 . Determine:Os pontos do hiperboloide x 2 + y 2 - z 2 = 0 onde o plano tangente é
Sejam S 1 e S 2 as superficies definidas por x 2 - y 2 + z 2 = 1 e x y + x z = 2 , respectivamente.Determine a equação do plano tangente à S 1 em ( 1,1 , 1 ) .
15. Uma peça de metal, com formato de cone de equação z 2 - x 2 9 - y 2 = 0 ,z ≥ 0 deve ser apoiada numa haste de ponto P 0 = 9,4 , 5 , de modo que a haste fique perpendicular à superfície do cone.a)