Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 14.4 - Ex. 37
Uma faixa interna de de largura é pintada na borda de um retângulo de dimensões por . Utilize os diferenciais para aproximar a área, em metros quadrados, da faixa pintada.
Passo 1
Opa, tudo beleza? Questãozinha de diferenciais com contexto, vamos lá!
A questão nos descreve um retângulo de dimensões cuja borda foi pintada da seguinte forma
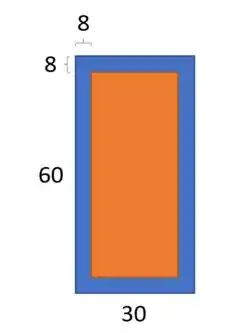
De forma que podemos dizer que
E em seguida o enunciado nos pede para usar o conceito de diferenciais para calcular a área da faixa pinta! Mas como fazemos isso?
Se a área do retângulo é por , nós podemos escrever o seguinte:
De forma que a diferencial será dada por
Então só precisamos calcular essas derivadas parciais e teremos nosso diferencia !
Passo 2
Para encontrar nós tratamos como constante, de forma que:
E da mesma forma encontramos como sendo
De forma que a nossa expressão fica
Substituindo todos os valores na expressão, ficamos com
Resposta
A área da faixa é