Enunciado
Cálculo Numérico - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.Revisão - Ex. 102
Os fatores funcionais de f(x) na tabela a seguir foram obtidos experimentalmente com a hipótese de que f é contínua em [1,3] , aproxime pela (a) regra do trapézio e (b) regra de Simpson.
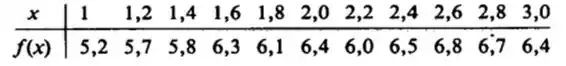
Passo 1
O que o enunciado nos pede é para utilizarmos uma regra já definida anteriormente na resolução de uma integral. A regra do trapézio definida no Teorema 5.10.1 nos diz que se a função f for contínua no intervalo fechado [a,b] e os números a = x0, x1, x2,..., xn=b formarem uma partição regular de [a,b] , então:
Ele também nos pede para utilizarmos uma outra regra já definida anteriormente na resolução de uma integral. A regra de Simpson definida no Teorema 5.10.4 nos diz que se a função f for contínua no intervalo fechado [a,b], n for um inteiro par e os números a = x0, x1, x2,..., xn=b formarem uma partição regular de [a,b] , então:
Passo 2
Letra (a)
Utilizando a regra do trapézio, vem:
[a,b] = [1 ,3] e n =11
Passo 3
Letra (b)
Utilizando a regra de Simpson , vem:
[a,b] = [1 ,3] e n =11
Resposta
(a)
(b)