Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.3 - Ex. 1
A figura abaixo mostra uma curva e um mapa de contorno de uma função cujo gradiente é contínuo. Determine
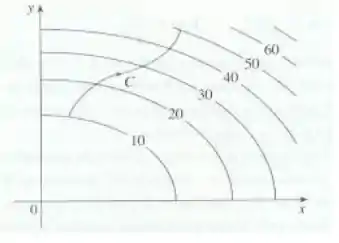
Passo 1
Oi galera, tudo bem? Nessa questão não temos que calcular quase nada! Saca só! Como a curva aparentemente é suave e uma vez que o gradiente é contínuo então o valor de vai ser apenas a diferença dos valores final e inicial das curvas de nível.
Passo 2
Vamos ver no gráfico como fica. A curva começa na curva de nível e termina na curva . Então:
É isso!
Vamos pra próxima?
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 27 e 28, encontre uma função potencial para F F = e x l n y i + e x y + s e n z j + ( y c o s z ) k
Ainda que eles não estejam definidos em todo o espaço R3, os campos associados com os Exercícios 18-22 são simplesmente conexose o teste dos componentes pode ser utilizado para mostrar que elessão con
O que é uma função potencial? Mostre com um exemplo comoencontrar uma função potencial para um campo conservativo
O que é uma superfície orientada? Como se pode calcular ofluxo de um campo vetorial tridimensional através de uma superfície orientada? Dê um exemplo.
Como se pode saber se um campo é conservativo?