Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.8 - Ex. 1
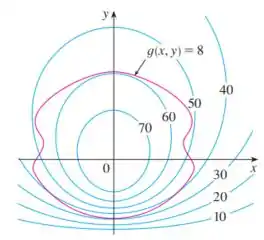
Na figura estão um mapa de contorno de e a curva de equação . Estime os valores máximo e mínimo de sujeita à restrição . Explique suas razões.
Passo 1
Opaa!! Tudo tranquilinho?? Bom... o enunciado nos deu esse gráfico de curvas de nível de uma função e a curva de equação :
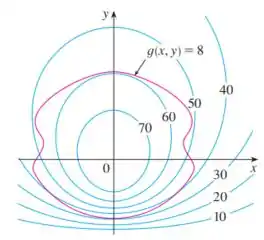
Queremos estimar valores máximo e mínimo de sujeita à restrição .
Mas como fazemos isso??
Bom... para encontrar esses valores, devemos achar o maior e o menor valor de tais que a curva tangencie a curva .
Sabendo disso, bora analisar juntos?? 😉
Passo 2
Pelo gráfico abaixo, vemos que a curva quase toca a curva de nível , veja:
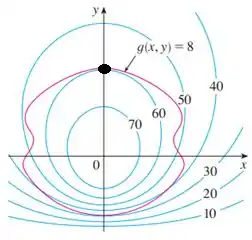
Assim, podemos assumir que o valor máximo de é aproximadamente .
Passo 3
Da mesma forma, vemos que o menor valor de para o qual as duas curvas se tangenciam parece ser , veja:
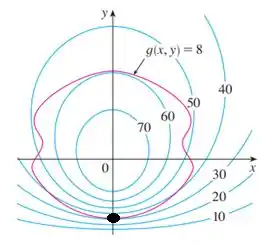
Portanto, estimamos que os valores máximo e mínimo de sujeita à restrição são, respectivamente, e .
Prontinho! Conseguimos!
Resposta
Máximo em e mínimo em .