Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.6 - Ex. 24
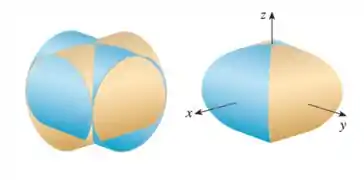
A figura mostra a superfície criada quando o cilindro intercepta o cilindro . Determine área dessa superfície
Passo 1
Faala, pessoal!
Vamos entender essa questão.
Ela pede pra gente achar a área de uma superfície. Pra isso, a gente pode usar a fórmula da área de uma superfície em um domínio :
Mas nesse caso, vamos usar uma fórmula equivalente, para superfície :
Antes de ir pras contas, vamos olhar pra superfície. Percebe que ela tem duas partes: uma laranja, e uma azul.
A parte laranja é a parte do cilindro dentro do cilindro .
Já a parte azul é o contrário: é a parte do cilindro dentro do .
Só que como ele são cilindros iguais, só muda o eixo que eles estão, essa figura vai ser simétrica! E a área de parte laranja é igual da parte azul!
Ou seja, pra gente encontrar a área, vamos calcular a da parte laranja e multiplicar por .
Pra achar essa área laranja, vamos começar definindo quem é , pra achar as derivadas parciais. Daí, jogamos na integral, e usamos o domínio pra achar uma integral iterada. Por fim, vamos calcular a integral!
Passo 2
Vamos começar olhando pra área laranja, que é a que vamos calcular:
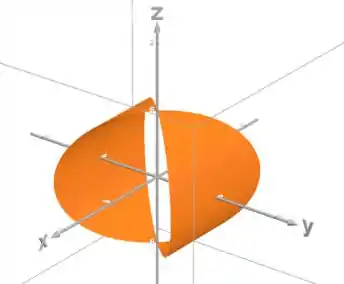
Ela é definida por
Tirando a raiz dos dois lados:
Percebe que a superfície tem duas partes iguais: uma positiva (), e parte negativa (). Vamos usar daqui pra frente só a parte positiva, e multiplicar por o resultado:
Então, vamos calcular as derivadas parciais.
Primeiro em função de , mantendo constante:
Agora em função de , vamos ter que usar a regra da cadeia:
Como a derivada de é ,
Colocando na fórmula:
Abrindo o quadrado, podemos cancelar a raiz com o quadrado:
Vamos colocar transformar esse termo dentro da raiz em uma fração única:
Então:
Passo 3
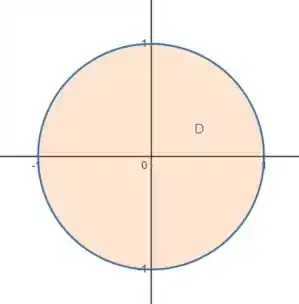
Agora vamos olhar para o domínio dessa superfície. Como estamos dentro do cilindro , nosso domínio é definido por:
Ele fica assim:
O domínio é limitado pela equação , que podemos reescrever como:
A expressão positiva representa a parte da direita da circunferência (), e negativa é a parte da esquerda:
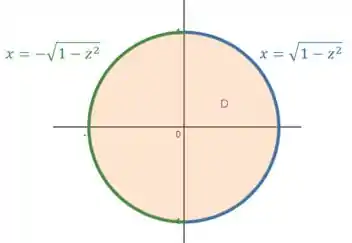
Então temos que está entre e , e entre as duas expressões:
Assim, conseguimos montar a integral iterada. Lembrando que como os limites de dependem de , integramos em função de primeiro:
Passo 4
Pra integrar isso, fazemos de fora pra dentro. Primeiro em função de , considerando constante:
Como o integrando só depende de , ele é constante em função de , e a integral fica:
Então:
Podemos colocar o pra fora da integral:
Passo 5
Aqui a gente precisa tomar um cuidado!
Você pode pensar em simplificar , mas não podemos fazer isso!
Nos extremos do intervalo de integração ( e ), esse termo vale , então teríamos uma indeterminação do tipo . Ou seja, isso é uma integral imprópria!
Pra resolver, temos que fazer o seguinte:
Agora podemos simplificar sem problema, porque no intervalo , o termo não vale :
Resolvendo nos limites:
Resolvendo o limite:
Relembrando, nós queremos a área da superfície :