Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.3 - Ex. 6
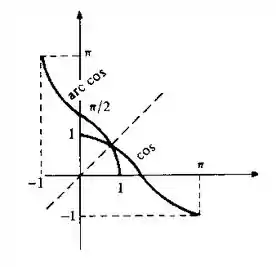
(Função arco-co-seno). A função , , é inversível e sua inversa é a função , .
- Calcule
- Esboce o gráfico de
Passo 1
- Vamos calcular , vamos ver as regras que vamos precisar para calcular as derivadas, vamos usar a regra da função trigonométrica:
Assim:
Vamos encontrar a inversa :
Agora vamos fazer uma manipulação através da identidade trigonométrica fundamental:
Substituindo em :
Com .
Passo 2
- Vamos esboçar o gráfico de atribuindo valores entre :
Resposta
Exercícios de Livros Relacionados
Se f x = x k , onde k é um inteiro positivo ímpar, prove que f não tem extremos relativos.
Ache a e b , tais que a função definida por f x = x 3 + a x 2 + b Tenha um extremo relativo em 2,3
a ) ache os extremos relativos de f pelo teste da derivada primeira b ) determine os valores nos quais os extremos relativos ocorrem c ) determine os intervalos nos quais f é crescente d ) determine o
A função f é crescente no intervalo I . Prove que a se g x = - f x , então g x será decrescente em I ; b se h x = 1 f x e f x0 em I , então h será decrescente em I .
Demonstre que funções crescentes e decrescentes são injetoras. Ou seja, demonstre que, para quaisquer x 1 e x 2 em I , x 1 ≠ x 2 implica f x 2 ≠ f x 1