Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.2 - Ex. 1b
- A função dada é integrável? Justifique.
b)
Passo 1
A função só é integrável se, f(x) for contínua no intervalo [a,b].
Como sei se é contínua?
Uma função é contínua quando eu consigo desenhar no papel o gráfico sem ter que tirar o lápis do papel. Em outras palavras, dado um intervalo, eu não tenho nenhum ponto que não satisfaça a equação (divisões por zero, tangente de .
Passo 2
Gráfico da função:
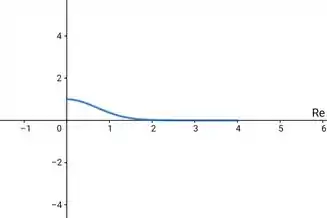
Para essa questão, f(x) é contínua no intervalo [0,4], pois não tenho nenhum x pertencente ao intervalo que zere o meu denominador, causando uma descontinuidade.
Resposta
Sim, é integrável, pois é contínua.
Exercícios de Livros Relacionados
Ache o valor exato da integral definida usando a relação entre soma de Riemann e integral definida. ∫ 1 2 x 3d x
Ache o valor exato da integral definida usando a relação entre soma de Riemann e integral definida. ∫ - 2 2 ( x 3 + 1 )d x
Ache o valor exato da integral definida usando a relação entre soma de Riemann e integral definida. ∫ - 2 1 ( x 4 )d x
int (x^3 + 5 x – 7) d x
Determine a integral definida: ∫ 2 - x 3 / 5 d x