Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.5 - Ex. 1b
- Verifique quais dos conjuntos a seguir são abertos em
b)
Passo 1
Se rearranjarmos a inequação pra fazer com que , vamos obter:
Portanto, graficamente, podemos desenhar a reta e considerar os pontos só acima dela. Afinal, veja que o ponto está acima da reta e é uma verdade que:
Graficamente então, teríamos:
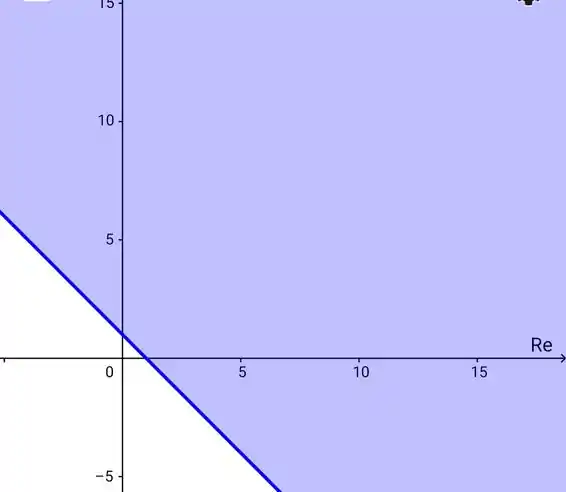
Como não tem o pontilhado, significa que a própria reta faz parte da solução, e logo o conjunto é fechado.
Resposta
Não é aberto.
Exercícios de Livros Relacionados
Verifique se a função é homogênea. Em caso afirmativo, determine o grau de homogeneidade. f x , y = 2 x 2 + y ² ²
Seja f: IR² → IR homogênea e suponha que f a , b = 0 para todo ( a , b ) , com a 2 + b 2 = 1 . Mostre que f x , y = 0 para todo x , y ≠ 0,0 .
Suponha que f: IR² → IR seja homogênea do grau 2 ef a , b = a para todo ( a , b ) , com a 2 + b 2 = 1 . Calcule: f 4 3 , 4
Suponha que f: IR² → IR seja homogênea do grau 2 ef a , b = a para todo ( a , b ) , com a 2 + b 2 = 1 . Calcule: f 4 3 , 4
Suponha que o conjunto B ⊆ R 2 não seja aberto. Pode-se concluir que B é fechado? Sim ou não? Justifique.