Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.8 - Ex. 36
A função definida por
é denominada função de Airy, em homenagem ao matemático e astrônomo inglês sir George Airy (1801-1892).
(a) Encontre o domínio da função de Airy.
(b) Trace as primeiras somas parciais na mesma tela.
(c) Se seu SCA tiver funções de Airy programadas, trace na mesma tela que as somas parciais na parte (b) e observe como as somas parciais aproximam .
Passo 1
Fala, amigos! Tudo numa boa?
Nossa questão tem 3 partes, vamos fazer 1 em cada passo. O enunciado traz uma função chamada Airy:
A letra a) pede pra gente achar o domínio dela, ou seja, os valores de que a função pode assumir. Para isso vamos usar o Teste da Razão, que vale a pena retomarmos aqui:
Se a série é absolutamente convergente (e, portanto, convergente). Caso a série é divergente e se o teste é inconclusivo.
A letra b) pede algumas somas parciais. Nesses caso, cada soma parcial será uma função diferente, por isso, ao invés de calcular valores, precisamos plotar gráficos.
A letra c) pede para plotarmos a função Airy junto com suas somas parciais (da letra b)) e observamos seu comportamento.
Vamos resolver cada uma!
Passo 2
- Beleza, galera? Pra encontrar o domínio dessa função, temos que encontrar pra quais valores de essa série converge. Então seria uma ótima ideia usar o Teste da Razão, já que temos termos exponenciais e que se multiplicam, e a divisão que o Teste da Razão traz simplifica isso. Mas como vamos usá-lo se não sabemos quem é e ?
Pra resolver isso, perceba que os termos da série podem ser definidos recursivamente, olha só:
Conhecemos o primeiro termo:
A partir do segundo termo, ou seja, de , cada termo tem multiplicado no numerador e o denominador pode ser escrito por:
Não se preocupe, é realmente difícil enxergar essa relação de recorrência, mas pode conferir se quiser!
Show! Agora sim podemos usar o Teste da Razão:
O termo era desconhecido, mas no final não fez diferença já que ele vai se cancelar na divisão . Tiramos o termo em função de do módulo, já que é sempre positivo e ficamos com o seguinte limite:
Como esse limite é sempre , que é menor do que , a série converge pra qualquer , ou seja, o domínio da função de Airy é .
Passo 3
(b) Beleza! Vamos traçar algumas somas parciais da série que define a função de Airy:
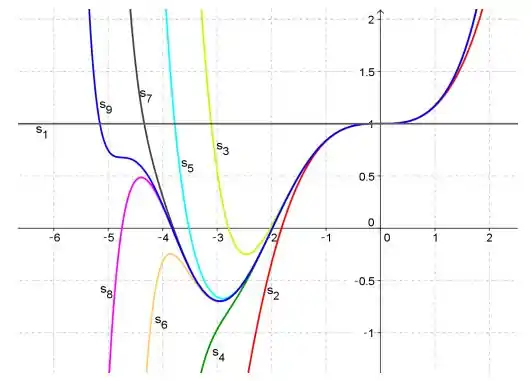
Passo 4
(c) Aqui podemos usar softwares como Maple, Mathematica e Derive. A função Airy juntamente com suas somas parciais ficam assim:
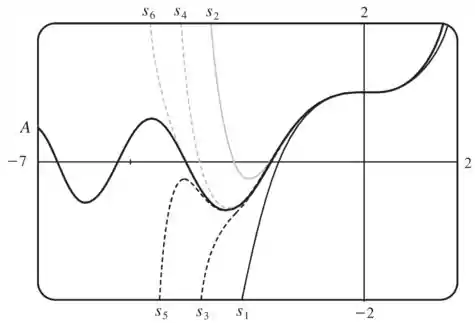
A linha mais grossa é a função Airy. são as somas parciais da nossa função. Note que conforme vai se aproximando de 0, as somas parciais se aproximam bastante da função.
Resposta
(a)