A involuta de uma circunferência é a curva traçada pelo ponto de extremidade de um fio quando o mesmo, mantido tenso, é desenrolado de um carretel fixo. Suponha que o centro do carretel está colocado na origem do plano e seu raio é , e que o fio começa a se desenrolar no ponto . Mostre que as equações paramétricas da involuta, ao desenrolar uma volta do fio no carretel, são:
Passo 1
A primeira coisa que nós temos que fazer é criarmos algumas referências utilizando as propriedades dos triângulos retângulos:
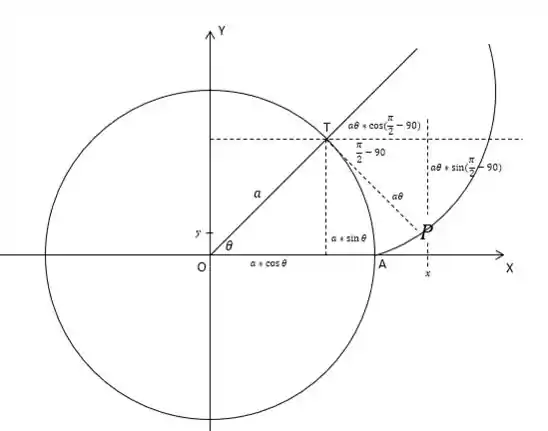
Passo 2
A partir delas conseguimos concluir que pode ser obtido através da seguinte soma:
Além disso, devemos nos lembrar da seguinte relação:
E em seguida aplicá-la em :
Passo 3
Já para , é fácil perceber que o mesmo pode ser obtido através da seguinte subtração:
Onde assim como no passo anterior, devemos nos lembrar da seguinte relação:
E em seguida aplicá-la em :
Resposta
Portanto, chegamos no seguinte par de equações paramétricas: