Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 2.8 - Ex. 18d
Identificar as curvas a seguir e parametrizá-las. Esboçar o seu gráfico.
d)
Passo 1
Então pessoal, para a curva que nos foi dada, como ela aparenta ser bem simples, então precisamos apenas isolar , se liga:
Pela equação que encontramos, podemos concluir que se trata de uma equação de parábola que não possui raízes reais!
Passo 2
Para uma função do segundo grau fica bem tranquilo parametriza-la, basta que coloquemos e em função de uma variável qualquer que chamaremos de , ok? Se fizermos , teremos a seguinte parametrização:
Por fim, se esboçarmos o gráfico dessa parábola, teremos o seguinte:
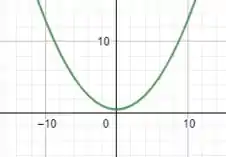
E esse é o nosso resultado, galera!
Resposta
Parábola:
Parametrização:
Exercícios de Livros Relacionados
Encontrar uma equação vetorial das seguintes curvas:e) x = e y ,z = e x
Encontrar uma equação vetorial das seguintes curvas:c) 2 x + 1 2 + y 2 = 10 ,z = 2
Determinar uma representação paramétrica da reta que passa pelo ponto A , na direção do vetor b → , onde:b) A 0 ,2 e b → = 5 i → - j →
Identificar as curvas a seguir e parametrizá-las. Esboçar o seu gráfico.e) y - 1 x - 1 = 0 ,x1
Encontrar uma equação vetorial das seguintes curvas:g) Segmento de reta de A 2 ,1 ,2 a B ( - 1 ,1 ,3 ) .