Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 10.1 - Ex. 20

Determine (del f)/(del x) e (del f)/(del y) sendo:

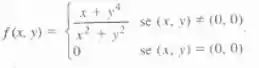
Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos essa equaçãozinha aii e depois dar o resultado. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser fazer nossa equaçãozinha.

Para x , y != 0,0

(del f)/(del x) = (del ((x + y^4)/(x^2 + y^2)))/(del x)

del ((x + y^4)/(x^2 + y^2)) = y ² - x^2 - 2 x y^4

(del f)/(del x) = (y^2 - x^2 - 2 x y^4)/((x^2 + y^2)^2)

Para x,y = 0,0, (del f)/(del x) é a derivada, nos dando que:

f (x , 0) = {[[x s e x != 0],[0 s e x = 0]])

lim ((f (x , 0) - f (0,0))/(x - 0)) = 1

(del f)/(del x) = {[[(y^2 - x^2 - 2 x y^4)/((x^2 + y^2)^2) , s e (x , y) != ( 0,0 )],[1 , s e (x , y) = ( 0,0 )]])

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

Para x , y != 0,0

(del f)/(del y) = (del ((x + y^4)/(x^2 + y^2)))/(del x)

del ((x + y^4)/(x^2 + y^2)) = 4 y ³ x ² + 2 y^5 - 2 y x

(del f)/(del y) = (4 y ³ x ² + 2 y^5 - 2 y x)/((x^2 + y^2)^2)

Para x,y = 0,0, (del f)/(del y) é a derivada, nos dando que:

f (0 , y) = {[[- 1 s e y != 0],[0 s e y = 0]])

lim ((f (0 , y) - f (0,0))/(y - 0)) = ...

OPA!! ESSE LIMITE NÃO EXISTE!!! Então, não podemos dizer que ela é definida naquele ponto.

(del f)/(del y) = (4 y ³ x ² + 2 y^5 - 2 y x)/((x^2 + y^2)^2)

Resposta

(del f)/(del x) = {[[(y^2 - x^2 - 2 x y^4)/((x^2 + y^2)^2) , s e (x , y) != ( 0,0 )],[1 , s e (x , y) = ( 0,0 )]])

(del f)/(del y) = (4 y ³ x ² + 2 y^5 - 2 y x)/((x^2 + y^2)^2)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a função produção de Cobb-Douglas P = b L α K β satisfaz a equação L ∂ P ∂ L + K ∂ P ∂ K = α + β P
Para o gás ideal do exercício 82, mostre queT (del P)/(del T) (del V)/(del T) = m R
Mostre que a função produção de Cobb-Douglas satisfaz P L , K 0 = C 1 K 0 L α resolvendo a equação diferencial d P d L = α P L
A lei dos gases para uma massa fixa m de um gás ideal à temperatura absoluta T , pressão P e volume V é P V = m R T , onde R é a constante do gás. Mostre que ∂ P ∂ V ∂ V ∂ T ∂ T ∂ P = - 1
Determine os sinais das derivadas parciais da função f cujo gráfico está mostrado.(a) f x 1,2 (b)f y 1,2