Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.6 - Ex. 3g
3. Inverter a ordem de integração:
g)
Passo 1
Pelos intervalos de integração, temos que:
Desses intervalos conseguimos obter 4 informações muito importantes:
Desenhando a região, obtemos o seguinte gráfico:
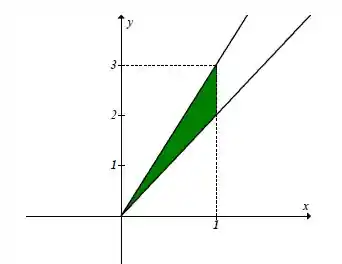
Nesse caso, temos o variando num intervalo numérico, o que denomina uma região do tipo 1. Logo, precisamos passar para uma região do tipo 2, onde meu varia em um intervalo numérico.
Passo 2
Na região do tipo 2, teremos o variando entre os seguintes intervalos:
Passo 3
Para escrever como uma região do tipo 2, nosso não terá mais uma variação numérica. Para obter a nova variação, pegue o gráfico e imagine uma seta indo no sentido positivo do eixo , da seguinte maneira:
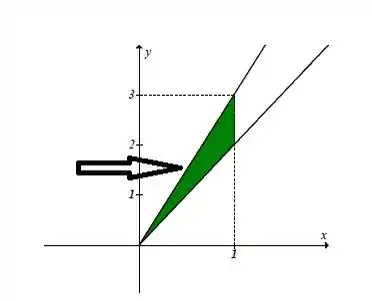
Assim, a seta toca em duas retas, que colocando em função de , são as seguintes:
Dessa forma, temos:
Entretanto, não é possível escrever tais intervalos. Por isso, precisamos dividir em duas figuras, para obter a nova área. Veja na figura abaixo representadas pelos números 1 e 2:
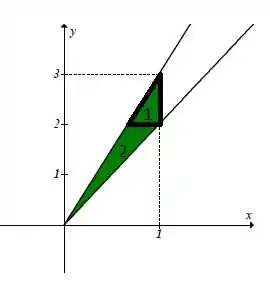
Dessa, forma teremos duas integrais, para cada figura, respeitando a região do topo 2: