Verifique que o Teorema de Stokes é verdadeiro para o campo vetorial dado e a superfície .
é o cone , , com orientação descendente.
Passo 1
E aii galera, beleza!?
Devemos verificar que o teorema de Stokes é verdadeiro para o seguinte campo vetorial:
Onde,
é o cone , , com orientação descendente.
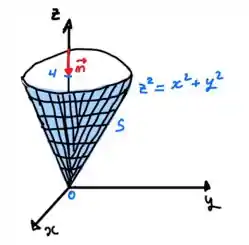
Vamos começar entendendo nossa região do cone.
Uma orientação descendente significa orientada para baixo, ou seja, o vetor normal no sentido negativo do eixo. Assim:
O Teorema de Stokes é definido como:
A integral dupla do rotacional de na superfície é igual a integral de linha de ao longo de uma curva fechada .
Para verificar que é verdadeiro, vamos ter que resolver cada integral, e ver se temos a mesma resposta.
Lembre-se que o rotacional é:
E,
Observe que precisamos fazer o determinante para achar o rotacional. Na segunda linha temos as derivadas em relação a , e na terceira linha os respectivos valores do campo vetorial, onde:
Já para a segunda parte da nossa integral, iremos fazer o seguinte:
Repare que precisamos achar uma parametrização para nossa região.
Como temos um cone:
Em , temo um círculo de raio :
A parametrização para um círculo é a seguinte:
Escrevendo em função de , temos que uma parametrização descendente é:
Agora que está mastigado as informações, deixo o resto com vocês.
Não tem erro, é só organizar as integrais.
Vamos nessa!
Passo 2
Vamos começar resolvendo essa integral:
Já sabemos que o rotacional é expresso como:
E que o campo vetorial é:
Onde temos:
Substituindo no rotacional, vamos ter:
Aplicando o determinante teremos:
Como nossa orientação é descendente, vamos ter o vetor normal no sentido negativo do eixo , conforme imagem:
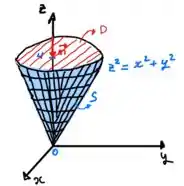
Logo, podemos escrever como:
Substituindo na integral, temos:
Assim temos que
Fazendo o produto escalar, temos:
Como temos a integral de , isso nos dá a própria área. Olhando a figura acima, sabemos que a área é igual a de um círculo de raio . Logo nossa resposta é:
Passo 3
Já para a segunda parte da nossa integral, iremos fazer o seguinte:
Como já vimos, podemos adotar a seguinte parametrização para o círculo:
Para achar , precisamos fazer a derivada de em relação a . Assim:
Precisamos também parametrizar . Assim temos que é:
Substituindo na integral, temos:
Fazendo o produto escalar temos:
Vamos utilizar a seguinte relação trigonométrica:
Assim, ficamos com:
Resolvendo essa integral, vamos ter:
Aplicando os limites de integração, temos que a integral de linha vale:
Veja, que realmente:
Logo, provamos que o teorema de Stokes é verdadeiro!
Resposta
O teorema de Stokes é verdadeiro!