Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 4.4 - Ex. 9

9. A janela de uma sala tem a forma de um retângulo com um triangulo isósceles no topo . Se o perímetro da janela é 12 m e esta deve coletar a maior a quantidade de energia possivel, mostre que o ângulo da base do triangulo é   π 6 radianos

Passo 1

Oii, nessa questão não é necessário descobrir todos os pontos críticos. A sacada é conseguir achar uma relação que nos ajude a encontrar o ângulo do nosso triângulo. Então nossa janela tem o seguinte formato

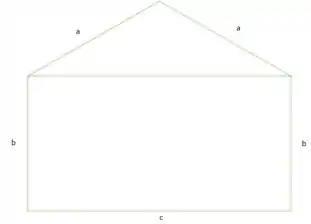
Passo 2

Podemos então montar as seguintes equações

P = 2 a + 2 b + c = 12  

Onde P é o perímetro da janela. Agora precisamos montar uma equação para a área. Vai ser então a área do quadrado mais a área do triângulo. Podemos achar a área do triângulo usando a formulinha

A T = b a s e ⋅ a l t u r a ⋅ 1 2

Visto que precisamos achar a altura, podemos montar um segundo triângulo com os seguintes lados

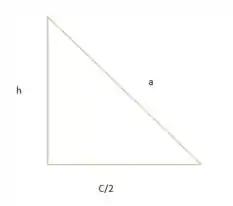
Por bhaskara descobrimos que

a 2 = h 2 + c 2 4

h = 4 a 2 - c 2 2

Com isso nossa área é

A = b c + c 4 4 a 2 - c 2

Passo 3

Vamos montar calcular então os gradientes dessas funções

∇ p = 2,2 , 1

∇ A = a c 4 a 2 - c 2 ,   c , b + 4 a 2 - c 2 4 - c ² 4 4 a 2 - c 2

Ajustando um pouco o gradiente de A , ficamos com

∇ A = a c 4 a 2 - c 2 ,   c , b + 2 a 2 - c 2 2 4 a 2 - c 2

Passo 4

Vamos montar o sistema de Lagrange

2 λ = a c 4 a 2 - c 2  

2 λ = c

λ = b + 2 a 2 - c 2 2 4 a 2 - c 2  

2 a + 2 b + c = 12

Beleza, ficamos com um sistema bem grande aqui. Vamos fazer o seguinte vamos usar a equação II em I

c = a c 4 a 2 - c 2  

a = 4 a 2 - c 2  

a 2 = 4 a 2 - c 2  

3 a 2 = c 2

Essa é a relação que precisamos. Visto que o triângulo é formado por a e c, só precisamos de uma relação entre essas duas variáveis.

Passo 5

Podemos escrever as seguintes relações do triangulo da nossa janela

h = a sen ⁡ θ

c 2 = a cos ⁡ θ

La em cima descobrimos uma relação entre h em função e a c. Vamos usar

4 a 2 - c 2 2 = a sen ⁡ θ

c 2 = a cos ⁡ θ

Vamos dividir a equação I pela II desse novo sistema

t g   θ =   4 a 2 - c 2 c

Vamos agora usar

3 a 2 = c 2

E com isso descobrir o ângulo

t g   θ =   4 a 2 - 3 a 2 3 a

t g   θ =   a 3 a

t g   θ =   1 3

E com isso descobrimos que o ângulo é

θ =   π 6    

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12. a) A função f x , y , z = l n x + ln ⁡ y + 3 ln ⁡ z Tem um máximo na porção da superfície esférica de equação x 2 + y 2 + z 2 = 5 a 2 Onde x0 ,y0,z0 e a é uma constante positiva. Encontre-ob) Usan
12. a) A função f x , y , z = l n x + ln ⁡ y + 3 ln ⁡ z Tem um máximo na porção da superfície esférica de equação x 2 + y 2 + z 2 = 5 a 2 Onde x0 ,y0,z0 e a é uma constante positiva. Encontre-ob) Usan
11. Encontre o mínimo de f x , y , z = x + y + z na superfície de equação x y z = k Onde x0,y0,z0 Use o resultado para mostrar que x y z 1 / 3 ≤ 1 3 x + y + z x ≥ 0,y ≥ 0,z ≥ 0
10. Determine a equação do plano que passa por 1,2 , 1 e determina com os planos coordenadas um tetraedro de volume maximo
15. Considere a curva C interseção do cilindro de equação x 2 12 + y 2 16 = 1 Com o plano 2 x + y+ z = 12 Determine as distancias máximas e mínimas dos pontos de C ao plano XY