Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.5 - Ex. 43

Um lado de um triângulo está aumentando a uma taxa de 3   c m / s e um segundo lado está decrescendo a uma taxa de 2   c m / s . Se a área do triângulo permanece constante, a que taxa varia o ângulo entre os lados quando o primeiro lado tem 20   c m de comprimento, o segundo lado tem   30   c m de comprimento e o ângulo é π / 6 ?

Passo 1

Vamos olhar para o triangulo

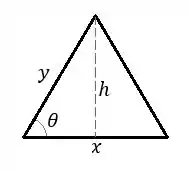
Temos que a sua área vai ser

A = 1 2 x h

Podemos ver que

sen ⁡ θ = h y

h = y sen ⁡ θ

Então a área é

A = 1 2 x y sen ⁡ θ

Passo 2

Como temos as taxas de crescimento dos lados pelo tempo e a área não varia, podemos dizer que

d A d t = 0

Podemos calcular d A / d t pela regra da cadeia na equação da área

d A d t = ∂ A ∂ x d x d t + ∂ A ∂ y d y d t + ∂ A ∂ θ d θ d t

∂ A ∂ x d x d t + ∂ A ∂ y d y d t + ∂ A ∂ θ d θ d t = 0

Nós queremos a taxa em que o ângulo varia, que é d θ / d t , as derivadas parciais nós podemos calcular

1 2 y sen ⁡ θ d x d t + 1 2 x sen ⁡ θ d y d t + 1 2 x y cos ⁡ θ d θ d t = 0

Multiplicando a equação por 2

y sen ⁡ θ d x d t + x sen ⁡ θ d y d t + x y cos ⁡ θ d θ d t = 0

Isolando d θ / d t

d θ d t = - y sen ⁡ θ d x d t + x sen ⁡ θ d y d t

d θ d t = - y sen ⁡ θ d x d t + x sen ⁡ θ d y d t x y cos ⁡ θ

Podemos colocar sen ⁡ θ em evidencia

d θ d t = - y d x d t + x d y d t sen ⁡ θ x y cos ⁡ θ

d θ d t = - y d x d t + x d y d t x y tg ⁡ θ

Passo 3

Substituindo os valores, quando x = 20 , y = 30 e θ = π / 6 , e temos também que as taxas d x d t = 3 e d y d t = - 2

d θ d t = - 30 ( 3 ) + 20 ( - 2 ) ( 20 ) ( 30 ) tg ⁡ π 6

d θ d t = - 90 - 40 600 3 3

d θ d t = - 3 3 6 ≈ - 0,05 r a d s

Resposta

d θ d t ≈ - 0,05 r a d s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que todas as funções dadas são diferenciáveis.Se u = f ( x , y ) , onde x = e s cos ⁡ t e y = e s sen ⁡ t , mostre que ∂ u ∂ x 2 + ∂ u ∂ y 2 = e - 2 s ∂ u ∂ s 2 + ∂ u ∂ t 2
Se um som com frequência f s for produzido por uma fonte se movendo ao longo de uma reta com velocidade v s e um observador estiver se movendo com velocidade v o ao longo da mesma reta a partir da dir
Use a regra da cadeia para determinar d z d t ou d w d t : z = x 2 y + x y 2 ,x = 2 + t 4,y = 1 - t 3
Use a regra da cadeia para determinar d z d t ou d w d t : z = x 2 + y 2 ,x = e 2 t,y = e - 2 t
Use a regra da cadeia para determinar d z d t ou d w d t . z = sin ⁡ x ⋅ cos ⁡ y x = π t,y = t