Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.8 - Ex. 2
Suponha que uma lâmina com densidade ocupe a região do plano . Calcule a massa total e as coordenadas do centro de massa de .
Passo 1
E aí jovem... Vamos fazer mais uma questãozinha de massa e centro de massa.
Lembrando que para encontrarmos a massa total do sistema, basta integrar a densidade :
Esta integral não tem muito segredo, podemos simplesmente substuir os limites em e ; como depende de , então vamos ter que resolver primeiro; repara só:
Vamos fazer o seguinte:
Começar pela primeira integral:
Dando uma ajeitada nisso:
E finalmente:
E a segunda integral:
Vamos ter novamente duas integrais:
Podemos fazer substituição trigonométrica na ; repara só:
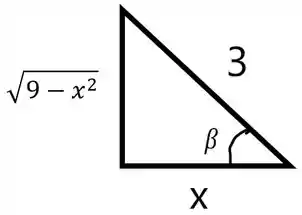
Ou seja, vamos fazer as seguintes substituições:
E, se , então :
Agora a integral do fica de certa forma fácil porque existe uma formulazinha:
Com isso, podemos voltar no triângulo e sumir com esse daí, trocando ele por alguma coisa que tenha :
Virj! E o ?? É só pegar o arc, olha só:
Sacou a idéia?
Portanto:
Onde:
E repare que o segundo termo ali, que mais assusta a gente, vai ser zero. Então teremos:
Retomando em :
Aquela segunda integralzinha ali ta de graça né?!
Eta tião.... da onde saiu esse mesmo?? De algum lugar lá em cima...
Podemos simplificar:
Graças a deus terminamos.... de achar a massa.
Ainda precisamos encontrar as coordenadas do centro de massa...
Passo 2
Vamos começar pelas coordenadas em
Então só precisamos encontrar:
Vamos nessa com foco, força e fé pra não errarmos nada:
Mais uma vez, dividindo em duas, com calma e paciência:
E aí aplicando os limites você vai perceber que fizemos tudo isso pra esse rolê dar zero...
Se não ficou claro pra você, vou te mostrar olha só:
Percebeu? Lembra da regrinha né?! Negativo vira positivo quando elevado a expoente par.
Mas calma que ainda falta aquela segunda integral:
Bora:
Crendeuspaitodopoderoso... Calma lá, vamos separar pra enxergar direitinho:
“vamos ter que fazer mais uma substituição trigonométrica??” Felizmente não...
Você lembra de uma propriedade de funções ímpares que diz o seguinte: “Seja uma função ímpar, então:
Ta começando a capitar? Mas como vamos saber se aquele diaxo ali é ímpar??
Então, pela definição de função ímpar temos o seguinte:
Vamos testar se isso vale na nossa função:
Vamo colocar
Ou seja, tamos uma função ímpar; então .
Nos resta:
É pra ficar feliz ou triste? Oh god.
A nossa coordenada em será:
Passo 3
Agora acabou, certo?? Nãããoo...Falta a coordenada em . É a mesmíssima coisa que acabamos de fazer:
Ou seja, só precisamos integrar:
Mais uma vez, o melhor jeito é abrir isso daí:
Acho que cê até decorou né?!
Jesus cristo, parece que piora cada vez mais:
Dessa vez não temos muita escapatória, teremos que fazer a substituição trigonométrica:
Mesma ideia do que fizemos no passo 1:
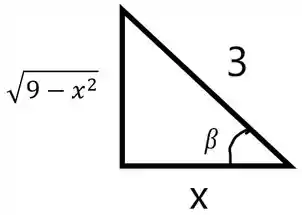
Ou seja, vamos fazer as seguintes substituições:
E, se , então :
Agora, existem diversas formas de resolver isso, vamos tentar achar o melhor caminho:
Existe uma formulazinha que diz o seguinte:
É chatinha, mas depois de tentar por vários caminhos percebi que esse é o melhor jeito:
Lembra que tomamos o seguinte:
E o ?Lembra que é só pegar o arc?
Com isso, a resposta do segundo termo ali é a mesma que achamos no passo 1:
e
Portanto:
Aplicando os limites:
Percebeu que o primeiro termo inteiro ali zera? Ou seja:
Pois é! Tá difícil. Mas vamos lá; ta acabando:
A segunda ali tá de graça:
E calma, que ainda falta a segunda integral:
Rapidex:
Teremos:
E finalmente:
Segura só mais um bocado, não é hora de errar agora:
Isso significa que:
E aí nossa segunda coordenada será:
Ufa! É muito provável que tenhamos errado algo; mas o que vale é a intenção. Né?! Hahahaha
Até a próxima!
Resposta
Portanto, encontramos que a massa total do sistema é:
E as coordenadas do Centro de massa serão: