Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.8 - Ex. 5
Suponha que uma lâmina com densidade ocupe a região do plano . Calcule a massa total e as coordenadas do centro de massa de .
é a região no primeiro quadrante, limitada pelas curvas e ;
Sendo:
Passo 1
Eaeee, Turubom?? Vamos atrás de mais umas massas e centros de massa.
Seguinte, nesse aqui temos que desenhar as curvas para enxergar o que tamo fazendo e o que tamo buscando.
Então vai lá:
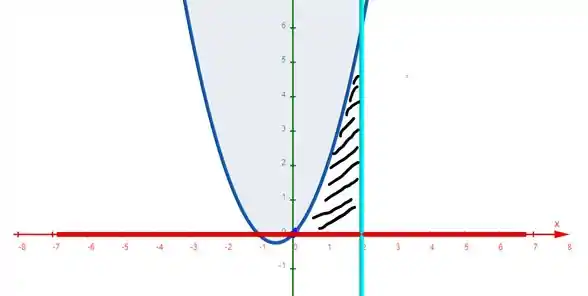
Chegou na mesma coisa aí?? Top.
Olha só, tenta perceber comigo que ta limitado da seguinte forma:
Beleza? Agora o , note que:
Isso porquê saindo de algum ponto do eixo entre 0 e 2, subindo no sentido positivo de em algum momento a gente bate de frente com a parábola. Ta comigo?
Bom, então beleza vamos tentar achar a massa dessa criança:
Aplicando os limites que encontramos:
Bora, foco, força e fé:
Aplicando isso:
Vamos dar uma ajeitada nisso; perceba que podemos simplificar isso tudo da seguinte forma:
E agora então é só integrar:
E aí finalmente:
Passo 2
Agora podemos encontrar as coordenadas do centro de massa desse rolê; lembrando que:
Vamos começar com , e resolver essa integral aí:
A primeira parte é igualzinho acabamos de fazer:
E então:
Tranquilo né? Agora a próxima:
Portanto, nossa coordenada em será:
Passo 3
Para terminar só falta a coordenada em . Só vamo.
Tudo o que precisamos fazer é calcular a integral:
Teremos:
Até aqui bem parecido com o que já fizemos:
E então:
Dessa vez vamos ter que abrir o produto notável:
Tomando cuidado é só integrar:
Finalmente encontramos:
Mas carmeia que ainda temos que dividir isso pela massa
E isso é tudo!! See u.
Resposta
Concluindo, a massa do sistema é ; enquanto que as coordenadas do centro de massa são: