Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 2
Marque o ponto cujas coordenadas esféricas são dadas. A seguir, encontre as coordenadas retangulares do ponto.
Passo 1
Olá, pessoal! Tudo bem?
A questão quer que a gente marque, ou seja, localize um ponto em coordenadas esféricas e depois pede para encontrarmos o equivalente desse ponto em coordenadas retangulares:
As relações entre coordenadas esféricas e coordenadas retangulares são dadas da seguinte forma:
Então, vamos precisar usar as equações acima para transformar nosso ponto em um ponto de coordenadas retangulares.
Bora lá!
Passo 2
Letra a:
Agora precisamos esboçar o ponto que nos foi dado. A distância da origem até o ponto é , e sabemos que é o ângulo que sai do eixo positivo pra baixo. Temos então quer dizer que estamos no plano . E com sabemos que, a partir do eixo , ele percorre em sentido anti horário, estando no eixo . Então o esboço é o seguinte:
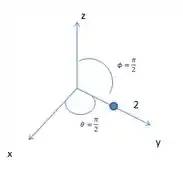
E como sabemos fica bem tranquilo determinar os pontos , é só substituir:
Então ficamos com:
Então esse ponto é
Beleza? Vamos para o próximo ponto?
Passo 3
Letra b:
Agora a distância até a origem é . O ângulo é , então estamos indo em sentido horário, rotacionando , o que nos deixa entre a parte negativa de e positiva de . O ângulo azimutal é , então estamos na porção superior do eixo . O esboço desse ponto é:
E como sabemos fica bem tranquilo determinar os pontos , é só substituir:
Substituindo os valores nas nossas equações:
Assim o ponto é