Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.1 - Ex. 51

Mostre que lim t → a ⁡ r t = b se e somente se para todo ε > 0 existe um número δ > 0 tal que

s e       0 < t - a < δ             e n t ã o           r t - b < ε

Passo 1

Eaeee, belezinha??? Bom... o enunciado quer que demonstremos o seguinte limite:

lim t → a ⁡ r t = b

Para todo ε > 0 existe um número δ > 0 tal que

s e       0 < t - a < δ             e n t ã o           r t - b < ε

Mas que variáveis são essas???

São basicamente as mesmas que estudamos no Cálculo 1 em Limites!!! Veja:

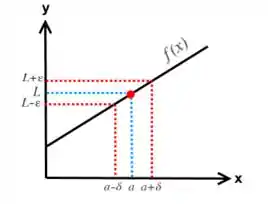
Assim, basta aplicarmos no campo vetorial com a curva r t !!

Assim, podemos reescrever algumas coisas dessa forma:

r t = x t ,       y t ,       z ( t )

Onde aplicando o limite:

lim t → a ⁡ r t = l i m t → a   x t ,       l i m t → a   y t ,       l i m t → a   z t

Logo, temos que provar esses limites!!!

Passo 2

Para b , temos:

b = b x ,       b y ,       b z

Onde:

  r t - b = x t - b x ,       y t - b y ,       z t - b z

Show! Agora podemos reduzir essa definição vetorial de limites à definição que já conhecemos.

Lembre-se que podemos afirmar o seguinte:

1 l i m t → a   x t = b x se e somente se para todo ε > 0 existe um número δ > 0 tal que

s e       0 < t - a < δ             e n t ã o           x t - b x < ε 3

(Sem perda de generalidade, pudemos dividir aquele último ε por 3 , e isso será útil mais tarde.)

Analogamente, podemos afirmar:

2 l i m t → a   y t = b y se e somente se para todo ε > 0 existe um número δ > 0 tal que

s e       0 < t - a < δ             e n t ã o           y t - b y < ε 3

3 l i m t → a   z t = b z se e somente se para todo ε > 0 existe um número δ > 0 tal que

s e       0 < t - a < δ             e n t ã o           z t - b z < ε 3

Passo 3

Agora, se a gente unir as três afirmações do passo anterior em uma só, fica equivalente a esta:

lim t → a ⁡ r t = b se e somente se para todo ε > 0 existe um número δ > 0 tal que:

s e       0 < t - a < δ             e n t ã o           x t - b x < ε 3       e       y t - b y < ε 3       e       z t - b z < ε 3

Ou seja, só precisamos terminar de mudar a última frase para chegar aonde queremos.

Então, note que, pelas propriedades de módulo, podemos escrever:

r t - b = x t - b x ,       y t - b y ,       z t - b z ≤ x t - b x + y t - b y + z t - b z < ε 3 + ε 3 + ε 3 = ε

Prontinho! Acabamos de concluir que a última frase que tínhamos escrito realmente implica:

r t - b < ε

Resposta

Demonstração

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Movimento ao longo de uma parábola Uma partícula se move ao longo do topo da parábola y 2 = 2 x da esquerda para a direita com módulo de velocidade constante de 5 unidades por segundo. Encontre a velo
Órbitas circularesMostre que um planeta em uma órbita circular se move com módulo de velocidade constante. (Sugestão: essa é uma consequência de uma das leis de Kepler).
Determine o comprimento do eixo maior da órbita da Terra utilizando a terceira lei de Kepler e o fato de que o período orbital da Terra é de 365,256 dias.
Suponha que r seja o vetor posição de uma partícula que se move ao longo de uma curva plana e dA/dt seja a taxa na qual o vetor varre a área. Sem introduzir coordenadas e assumindo que as derivadas ne
Terceira lei de KeplerComplete a dedução da terceira lei de Kepler (a parte seguinte à Equação 10).