Mostre que f ∗ f não precisa ser não negativa usando o exemplo.
Passo 1
Avalie a integral de convolução f∗f.
Passo 2
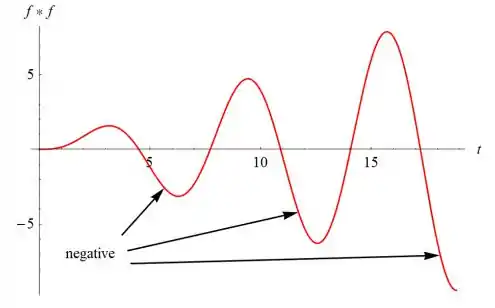
Como mostra o gráfico de versus t, f∗f não é necessariamente não negativo.
Mostre que f ∗ f não precisa ser não negativa usando o exemplo.
Avalie a integral de convolução f∗f.

Como mostra o gráfico de versus t, f∗f não é necessariamente não negativo.