Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.2 - Ex. 14
Mostre que a reta normal à cicloide (exemplo , seção ) em um ponto contém o ponto de tangência no eixo da circunferência rolante que passa por .
Passo 1
Pra começar, vamos pegar a parametrização da cicloide:
A gente precisa de informações sobre a reta normal, certo? Antes disso, vamos falar da inclinação da reta tangente. Derivando:
Seja o valor do parâmetro que define o ponto , o vetor tangente à nesse ponto será:
Passo 2
Beleza, agora pensa comigo, se a circunferência tangencia o eixo dessa forma:
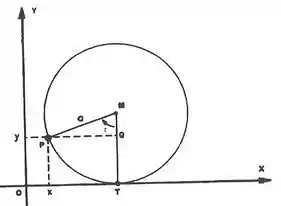
As coordenadas, do ponto de tangência serão:
E os do ponto P serão:
Sendo assim, a inclinação do vetor em determinado será:
Se a nossa reta normal tem que passar tanto por quanto por , então a inclinação do vetor normal tá na mão:
Passo 3
Agora a gente junta as informações dos dois passos. Se esses vetores são realmente os vetores normal e tangente, o produto escalar deles deve ser pra qualquer . Vamos provar isso:
Dividindo os dois lados por temos:
Resposta
O do vetor que passa pelo ponto de tangência e pelo ponto de tangência da circunferência rolante com o eixo é de fato o vetor diretor da reta normal uma vez que o produto escalar desse vetor com ovetor diretor da reta tangente é nulo.