Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 7c
Olhando para o gráfico de , estude o sinal de .
Passo 1
O Gráfico da reta é dado por:
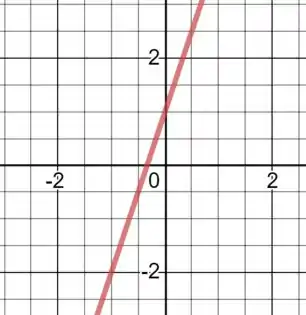
Passo 2
A reta encontra o eixo em então e, portanto, quando .
Por ser crescente, antes do ponto só temos valores de menores que zero de depois de todo os valore são maiores que zero. Então:
para
para
Resposta
para
para
Exercícios de Livros Relacionados
Encontre o domínio da função f p = 2 - p
Encontre o domínio da função f t = 2 t - 1 3
Encontre o domínio da função g t = 3 - t - 2 + t
Encontre o domínio da função f x = x + 4 x 2 - 9
31 - 37 Encontre o domínio da função h x = 1 x 2 - 5 x 4